题目内容
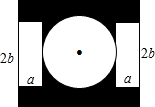 某学校办公楼前有一长为m,宽为n的长方形空地,在中心位置留出一个直径为2b的圆形区域建一个喷泉,两边是两块长方形的休息区,阴影部分为绿地
某学校办公楼前有一长为m,宽为n的长方形空地,在中心位置留出一个直径为2b的圆形区域建一个喷泉,两边是两块长方形的休息区,阴影部分为绿地(1)用字母和π的式子表示阴影部分的面积;
(2)当m=8,n=6,a=1,b=2时,阴影部分的面积是多少?(π取3)
考点:列代数式,代数式求值
专题:
分析:(1)阴影部分的面积=长方形空地的面积-圆的面积-两块长方形的休息区的面积;
(2)把m=4,n=3,a=1,b=2代入(1)中所求的代数式,计算即可求解.
(2)把m=4,n=3,a=1,b=2代入(1)中所求的代数式,计算即可求解.
解答:解:(1)∵长方形空地的长为m,宽为n,
∴长方形空地的面积=mn,
∵圆的直径为2b,
∴圆的面积=πb2,
∵长方形休息区的长为2b,宽为a,
∴两块长方形的休息区的面积=4ab,
∴阴影部分的面积=mn-πb2-4ab;
(2)当m=8,n=6,a=1,b=2时,
阴影部分面积=mn-πb2-4ab=8×6-3×22-4×1×2=48-12-8=28.
∴长方形空地的面积=mn,
∵圆的直径为2b,
∴圆的面积=πb2,
∵长方形休息区的长为2b,宽为a,
∴两块长方形的休息区的面积=4ab,
∴阴影部分的面积=mn-πb2-4ab;
(2)当m=8,n=6,a=1,b=2时,
阴影部分面积=mn-πb2-4ab=8×6-3×22-4×1×2=48-12-8=28.
点评:本题考查了根据题意列代数式和求代数式的值,解答此类问题理清题意是关键.

练习册系列答案
相关题目
已知反比例函数和正比例函数在第一象限的交点为A(1,3),则在第三象限的交点B为( )
| A、(-1,-3) |
| B、(-3,-1) |
| C、(-2,-6) |
| D、(-6,-2) |
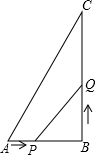 在△ABC中,∠B=90°,AB=6cm,BC=12cm.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B沿BC向点C以2cm/s的速度移动.如果点P、Q分别从A、B同时出发.
在△ABC中,∠B=90°,AB=6cm,BC=12cm.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B沿BC向点C以2cm/s的速度移动.如果点P、Q分别从A、B同时出发.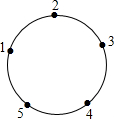 圆上有五个点,这五个点将圆分成五等份(每一份称为一段弧长),把这五个点按顺时针方向依次编号为1,2,3,4,5,若从某一点开始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,则称这种走法为一次“移位”.如:小明在编号为3的点,那么他应走3段弧长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的点,然后从1→2为第二次“移位”.若小明从编号为4的点开始,第2015次“移位”后,他到达编号为
圆上有五个点,这五个点将圆分成五等份(每一份称为一段弧长),把这五个点按顺时针方向依次编号为1,2,3,4,5,若从某一点开始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,则称这种走法为一次“移位”.如:小明在编号为3的点,那么他应走3段弧长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的点,然后从1→2为第二次“移位”.若小明从编号为4的点开始,第2015次“移位”后,他到达编号为 已知△ACD∽△BCA,若CD=4,CB=9,则AC=
已知△ACD∽△BCA,若CD=4,CB=9,则AC=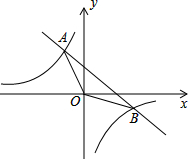 如图,已知一次函数y=kx+b(k≠0)的图象与反比例函数
如图,已知一次函数y=kx+b(k≠0)的图象与反比例函数