题目内容
在⊙O中,弦AB所对的劣弧为圆周的
,圆的半径等于12,则圆心角∠AOB= ;弦AB的长为 .
| 1 |
| 4 |
考点:圆心角、弧、弦的关系
专题:计算题
分析:根据圆心角、弧、弦的关系可得到∠AOB=
×360°=90°,然后根据等腰直角三角形的性质易得AB的长.
| 1 |
| 4 |
解答:解:如图,
∵弦AB所对的劣弧为圆周的
,
∴∠AOB=
×360°=90°,
∵OA=OB,
∴△AOB为等腰直角三角形,
∴AB=
OA=12
.
故答案为90°,12
.

∵弦AB所对的劣弧为圆周的
| 1 |
| 4 |
∴∠AOB=
| 1 |
| 4 |
∵OA=OB,
∴△AOB为等腰直角三角形,
∴AB=
| 2 |
| 2 |
故答案为90°,12
| 2 |
点评:本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.也考查了等腰直角三角形.

练习册系列答案
相关题目
 如图,△ABC∽△AED,∠ADE=80°,∠A=60°,则∠B等于( )
如图,△ABC∽△AED,∠ADE=80°,∠A=60°,则∠B等于( )| A、40° | B、50° |
| C、60° | D、80° |
 如图,已知:0<A<90°,则下列各式成立的是( )
如图,已知:0<A<90°,则下列各式成立的是( )| A、sinA=cosA |
| B、sinA>cosA |
| C、sinA>tanA |
| D、sinA<cosA |
 如图,在△ABC中,∠ABC=90°,tanA=
如图,在△ABC中,∠ABC=90°,tanA=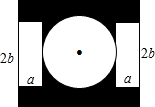 某学校办公楼前有一长为m,宽为n的长方形空地,在中心位置留出一个直径为2b的圆形区域建一个喷泉,两边是两块长方形的休息区,阴影部分为绿地
某学校办公楼前有一长为m,宽为n的长方形空地,在中心位置留出一个直径为2b的圆形区域建一个喷泉,两边是两块长方形的休息区,阴影部分为绿地