Question

12．平面直角坐标系中，A（-1，3），C（2，-1），则以AC为对角线的正方形ABCD的顶点B、D坐标分别为多少？

Answer 1

分析 如图，过点E作FK∥x轴，BF⊥FK于F，DK⊥FK于K，AM⊥FK于M．首先求出点E坐标，推出AM=2，EM=$\frac{3}{2}$，由△AME≌△EKD≌△EFB，可得EK=EF=AM=2，DK=BF=EM=$\frac{3}{2}$，由此即可解决问题．

解答 解：如图，过点E作FK∥x轴，BF⊥FK于F，DK⊥FK于K，AM⊥FK于M．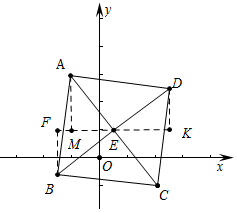

∵四边形ABCD是正方形，A（-1，3），C（2，-1），
∴EA=EC=EB=ED，E（$\frac{1}{2}$，1），
∴AM=2，EM=$\frac{3}{2}$，
由△AME≌△EKD≌△EFB，可得EK=EF=AM=2，DK=BF=EM=$\frac{3}{2}$，
∴D（$\frac{5}{2}$，$\frac{5}{2}$），B（-$\frac{3}{2}$，-$\frac{1}{2}$）或B（$\frac{5}{2}$，$\frac{5}{2}$），D（-$\frac{3}{2}$，-$\frac{1}{2}$）．

点评 本题考查正方形的性质、全等三角形的判定和性质、中点坐标公式等知识，解题的关键是学会添加常用辅助线构造全等三角形解决问题，属于中考常考题型．