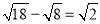题目内容
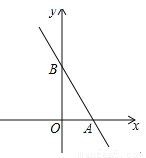
如图,直线l的解析式为y=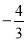 x+b,它与坐标轴分别交于A、B两点,其中B坐标为(0,4).
x+b,它与坐标轴分别交于A、B两点,其中B坐标为(0,4).
(1)求出A点的坐标;
(2)若点 P在y轴上,且到直线l的距离为3,试求点P的坐标;
(3)在第一象限的角平分线上是否存在点Q使得∠QBA=90°?若存在,求点Q的坐标;若不存在,请说明理由.
(4)动点C从y轴上的点(0,10)出发,以每秒1cm的速度向y轴负半轴方向运动,求出点C运动中所有可能的时间t值,使得△ABC为轴对称图形.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


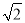 ,AD=1,则四边形ACEN的面积为 .
,AD=1,则四边形ACEN的面积为 .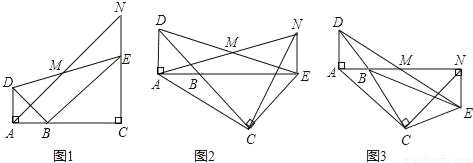
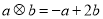 ,则
,则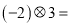 __________.
__________.
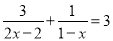
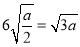 B.
B. 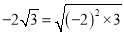
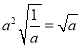 D.
D.