题目内容

11．时钟显示为8：20时，时针与分针所夹的角是（　　）
A．130°B．120°C．110°D．100°

分析 根据时针与分针相距的份数乘以每份的度数，可得答案．

解答 解：8：20时，时针与分针相距4+$\frac{20}{60}$=$\frac{13}{3}$份，
8：20时，时针与分针所夹的角是30×$\frac{13}{3}$=130°，
故选：A．

点评 本题考查了钟面角，确定时针与分针相距的分数是解题关键．

练习册系列答案
相关题目
2．计算或化简：
（1）（0.25a2b-$\frac{1}{2}$a3b2-$\frac{1}{6}$a4b3）÷（-0.5a2b）
（2）（x+2y-3）（x-2y+3）
（3）（$\frac{2a}{b}$）2$•\frac{1}{a-b}$-$\frac{a}{b}$$÷\frac{b}{4}$
（4）（$\frac{{a}^{2}+1}{a-1}$-a+1）$÷\frac{4{a}^{2}}{{a}^{2}-1}$．
19．将抛物线y=x2-2x+2先向右平移3个单位长度，再向上平移2个单位长度，则经过这两次平移后所得抛物线的顶点坐标是（　　）
A．（-2，3）B．（-1，4）C．（3，4）D．（4，3）
6．如图，已知⊙O是△ABC的外接圆，若弦BC等于⊙O的半径，则∠BAC等于（　　）
A．30°B．45°C．60°D．20°
16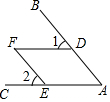．如图，点D、E分别在AB、AC上，若∠1=∠2=∠A=∠F，下列推理正确的是（　　）
A．由∠1=∠F得DF∥AEB．由∠2=∠F得AD∥EFC．由∠1=∠A得DF∥AED．由∠2=∠A得DF∥AE
3．已知方程组$\left\{\begin{array}{l}{x-y=5}\\{3x+2y=-1}\end{array}\right.$，则2（x-y）-3（3x+2y）的值为（　　）
A．11B．12C．13D．14
20．因式分解：
（1）（a+1）x-a-1          
（2）ax3-2ax2y+axy2．
1．已知甲、乙两个函数图象上的部分点的横坐标x与纵坐标y如表所示．若在实数范围内，甲、乙的函数值都随自变量的增大而减小，且两个图象只有一个交点，则关于这个交点的横坐标a，下列判断正确的是（　　）
x-2024
y甲5432
y乙653.50
A．a＜-2B．-2＜a＜0C．0＜a＜2D．2＜a＜4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网