题目内容
17．
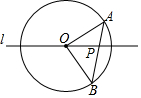如图，已知点A、B为⊙O上的两点，且∠A=40°，直线l经过圆心O，与AB相交于点P，若直线l绕点O旋转，当△OBP为等腰三角形时，∠AOP=60°．
分析 根据等腰三角形的性质得出∠BOP=∠B=40°，根据三角形内角和定理求得∠AOB=100°，即可求得∠AOP=∠AOB-∠BOP=60°．
解答 解：∵点A、B为⊙O上的两点，
∴OA=OB，
∵∠A=40°，
∴∠B=40°，
∴∠AOB=180°-2×40°=100°
∵当△OBP为等腰三角形时，OP=BP，
∴∠BOP=∠B=40°，
∴∠AOP=∠AOB-∠BOP=100°-40°=60°，
故答案为60°．
点评 本题考查了等腰三角形的性质，三角形内角和定理，熟练掌握性质定理时解题的关键．
练习册系列答案
优生乐园系列答案
相关题目
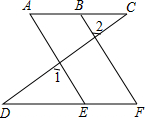如图，∠1=∠2，∠A=∠F，求证：∠C=∠D．
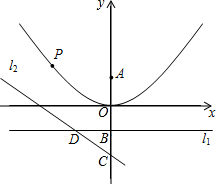如图，在平面直角坐标系中，直线l1过点B（0，-1），且平行于x轴，直线l2过点C（0，-2），交直线l1于点D，$\frac{BD}{BC}=\frac{4}{3}$，点A与点B关于x轴对称，点P为抛物线y=$\frac{1}{4}$x2上一动点，PQ⊥l1于点Q．
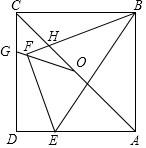在正方形ABCD中，AB=6，点E在边AD上，DE=$\frac{1}{3}$AD．连接BE，将△ABE沿BE翻折，点A落在点F处，BF与AC交于点H，点O是AC的中点，连接OF并延长交CD于点G，则四边形GFHC的面积是$\frac{5184}{2431}$．