题目内容
17.如图1是一个长为2a,宽为2b的长方形(a>b),沿图中虚线用剪刀均匀分成四块相同小长方形,然后按图2方式拼成一个大正方形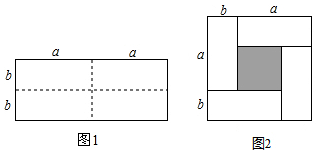
(1)你认为图2中大正方形的边长为(a+b);小正方形(阴影部分)的边长为(a-b).(用含a、b代数式表示)
(2)仔细观察图2,利用图2中存在的面积关系,直接写出下列三个代数式:(a-b)2,(a+b)2,4ab之间的等量关系
(3)利用(2)中得出的结论解决下面的问题:已知a+b=7,ab=6,求代数式(a-b)的值.
分析 (1)本题可以直接求阴影部分正方形的边长,计算面积;也可以用正方形的面积减去四个小长方形的面积,得阴影部分的面积;
(2)由(1)即可得出三个代数式之间的等量关系;
(3)将a+b=7,ab=6,代入三个代数式之间的等量关系即可求出(a-b)2的值.
解答 解:(1)图2中大正方形的边长为(a+b);小正方形(阴影部分)的边长为(a-b);
(2)三个代数式之间的等量关系是:(a+b)2=(a-b)2+4ab;
(3)(a-b)2=(a+b)2-4ab=25,所以a-b=5;
故答案为:(a+b);(a-b).
点评 本题主要考查公式变形能力,如何准确地确定三个代数式之间的等量关系是解题的关键.

练习册系列答案
相关题目
8. 如图所示:∠CAB=∠BCD,AD=2,BD=4,则BC=( )
如图所示:∠CAB=∠BCD,AD=2,BD=4,则BC=( )
 如图所示:∠CAB=∠BCD,AD=2,BD=4,则BC=( )
如图所示:∠CAB=∠BCD,AD=2,BD=4,则BC=( )| A. | $2\sqrt{2}$ | B. | $2\sqrt{6}$ | C. | 3 | D. | 6 |
12. 如图,△ABC和△EFC都是等边三角形,AD是△ABC的高,AB=4,若点E在直线AD上运动,连接DF,则在点E运动过程中,线段DF的最小值是( )
如图,△ABC和△EFC都是等边三角形,AD是△ABC的高,AB=4,若点E在直线AD上运动,连接DF,则在点E运动过程中,线段DF的最小值是( )
 如图,△ABC和△EFC都是等边三角形,AD是△ABC的高,AB=4,若点E在直线AD上运动,连接DF,则在点E运动过程中,线段DF的最小值是( )
如图,△ABC和△EFC都是等边三角形,AD是△ABC的高,AB=4,若点E在直线AD上运动,连接DF,则在点E运动过程中,线段DF的最小值是( )| A. | 1 | B. | 2 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
2.已知a-b=10,ab=5,则a2+b2的值为( )
| A. | 95 | B. | 110 | C. | 90 | D. | 105 |
7. 如图,在Rt△ABC中,∠B=90°,AB=3,AC=5,点E在BC上,将△ABC沿AE折叠,使点B落在AC边上的点B′处,则BE的长为( )
如图,在Rt△ABC中,∠B=90°,AB=3,AC=5,点E在BC上,将△ABC沿AE折叠,使点B落在AC边上的点B′处,则BE的长为( )
 如图,在Rt△ABC中,∠B=90°,AB=3,AC=5,点E在BC上,将△ABC沿AE折叠,使点B落在AC边上的点B′处,则BE的长为( )
如图,在Rt△ABC中,∠B=90°,AB=3,AC=5,点E在BC上,将△ABC沿AE折叠,使点B落在AC边上的点B′处,则BE的长为( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | 2 |

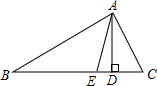 如图所示,已知在△ABC中,AD⊥BC于D,AE平分∠BAC,若∠B=28°,∠DAE=16°,求∠C的度数.
如图所示,已知在△ABC中,AD⊥BC于D,AE平分∠BAC,若∠B=28°,∠DAE=16°,求∠C的度数.