题目内容
12.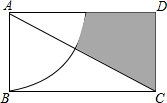 如图,矩形ABCD的长AD为2$\sqrt{3}$,宽AB为2,若以A点为圆心,AB为半径作出扇形,则图中阴影部分的面积为2$\sqrt{3}$-$\frac{1}{3}$π.(用含π的式子表示)
如图,矩形ABCD的长AD为2$\sqrt{3}$,宽AB为2,若以A点为圆心,AB为半径作出扇形,则图中阴影部分的面积为2$\sqrt{3}$-$\frac{1}{3}$π.(用含π的式子表示)
分析 先根据锐角三角函数的定义求出∠DAC的度数,再由S阴影=S矩形ABCD-S△ABC-S扇形即可得出结论.
解答 解:∵AD=2$\sqrt{3}$,AB=2,
∴tan∠DAC=$\frac{CD}{AD}$=$\frac{2}{2\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴∠DAC=30°,
∴S阴影=S矩形ABCD-S△ABC-S扇形
=2×2$\sqrt{3}$-$\frac{1}{2}$×2×2$\sqrt{3}$-$\frac{30π×{2}^{2}}{360}$
=2$\sqrt{3}$-$\frac{1}{3}$π.
故答案为:2$\sqrt{3}$-$\frac{1}{3}$π.
点评 本题考查的是扇形面积的计算,熟记扇形的面积公式是解答此题的关键.

练习册系列答案
相关题目
20.若x2+kx+81是完全平方式,则k的值应是( )
| A. | 16 | B. | 18 | C. | -18 | D. | 18或-18 |
7.在?ABCD中,BD、AC是对角线,下列结论不正确的是( )
| A. | 当AB=BC时,?ABCD是菱形 | B. | 当∠ABC=90°时,?ABCD是矩形 | ||
| C. | 当AC⊥BD时,?ABCD是菱形 | D. | 当AC=BD时,?ABCD是正方形 |
 如图,在平面直角坐标系中,点A(10,0),B(0,8),C(0,4),D(2,4).点P从B点出发沿线段BA向点A匀速运动.点Q从点A沿线段AD匀速运动,点P,Q同时到达各自的终点.设点P的横坐标为m,过点P作x轴,y轴的垂线,垂足分别为E,F,设矩形PEOF与梯形AOCD重叠部分的面积为S
如图,在平面直角坐标系中,点A(10,0),B(0,8),C(0,4),D(2,4).点P从B点出发沿线段BA向点A匀速运动.点Q从点A沿线段AD匀速运动,点P,Q同时到达各自的终点.设点P的横坐标为m,过点P作x轴,y轴的垂线,垂足分别为E,F,设矩形PEOF与梯形AOCD重叠部分的面积为S