题目内容
19. 如图,∠AOB=110°,OD平分∠BOC,OE平分∠AOC.
如图,∠AOB=110°,OD平分∠BOC,OE平分∠AOC.(1)求∠EOD的度数.
(2)若∠BOC=90°,求∠AOE的度数.
分析 (1)由OD平分∠BOC,OE平分∠AOC,可知∴∠EOD=∠COD+∠COE=$\frac{1}{2}$(∠BOC+∠AOC)=$\frac{1}{2}$∠AOB=55°;
解答 解:(1)∵OD平分∠BOC,OE平分∠AOC,
∴∠COD=$\frac{1}{2}$∠BOC,∠COE=$\frac{1}{2}$∠AOC,
∴∠EOD=∠COD+∠COE
=$\frac{1}{2}$(∠BOC+∠AOC)
=$\frac{1}{2}$∠AOB
=55°
(2)由于∠AOC=∠AOB-∠BOC=110°-90°=20°,
∵OE平分∠AOC,
∴∠AOE=$\frac{1}{2}$∠AOC=10°
点评 本题考查角的计算,涉及角平分线的性质,属于基础题型.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
14.当太阳光线与地面成40°角时,在地面上的一棵树的影长为10m,树高h(单位:m)的范围是( )
| A. | 3<h<5 | B. | 5<h<10 | C. | 10<h<15 | D. | 15<h<20 |
8.下列去括号错误的是( )
| A. | 3a2-(2a-b+5c)=3a2-2a+b-5c | B. | 5x2+(-2x+y)-(3z-a)=5x2-2x+y-3z+a | ||
| C. | 2m2-3(m-1)=2m2-3m-1 | D. | -(2x-y)-(-x2+y2)=-2x+y+x2-y2 |
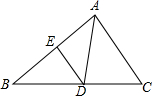 如图,△ABC中,D是BC上一点,∠DAC=∠B,E为AB上一点.
如图,△ABC中,D是BC上一点,∠DAC=∠B,E为AB上一点.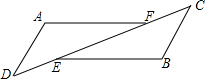 如图△ADF和△BCE中,∠A=∠B,点D、E、F、C在同一直线上,有如下三个关系式:①AD=BC;②DE=CF;③BE∥AF.
如图△ADF和△BCE中,∠A=∠B,点D、E、F、C在同一直线上,有如下三个关系式:①AD=BC;②DE=CF;③BE∥AF.