题目内容
4．先解方程，再类比方程的解法解不等式（1）2x-3=$\frac{x+1}{3}$；
（2）2x-3＜$\frac{x+1}{3}$．
分析 （1）利用解一元一次方程的方法与步骤求得未知数的值即可；
（2）类比方程的解法利用不等式的性质解不等式即可．
解答 （1）2x-3=$\frac{x+1}{3}$
解：3（2x-3）=x+1
6x-9=x+1
6x-x=1+9
5x=10
x=2；
（2）2x-3＜$\frac{x+1}{3}$
解：3（2x-3）＜x+1
6x-9＜x+1
6x-x＜1+9
5x＜10
x＜2．
点评 此题考查积额一元一次方程与不等式，掌握解方程与解不等式的步骤与方法是解决问题的关键．
练习册系列答案
学而优暑期衔接南京大学出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
15．
如图，AB∥CD，直线EF与AB，CD相截，若∠5=62°，则∠4的度数是（ ）
如图，AB∥CD，直线EF与AB，CD相截，若∠5=62°，则∠4的度数是（ ）| A． | 28° | B． | 62° | C． | 118° | D． | 146° |
9．
已知抛物线y=ax2+bx+c的部分图象如图所示，若y＜0，则x的取值范围是（ ）
已知抛物线y=ax2+bx+c的部分图象如图所示，若y＜0，则x的取值范围是（ ）| A． | -1＜x＜3 | B． | -1＜x＜4 | C． | x＜-1或 x＞4 | D． | x＜-1或 x＞3 |
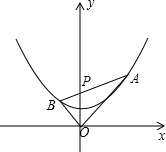已知点P坐标为（0，2），点A是抛物线y=$\frac{1}{4}$x2+1上在第一象限内的一个动点，直线AP与抛物线的另一个交点为点B，连结AO，BO．