Question

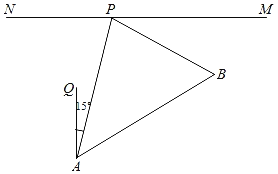
【题目】如图，在一条东西走向的公路MN的同侧有A，B两个村庄，村庄B位于村庄A的北偏东60°的方向上（∠QAB＝60°），公路旁的货站P位于村庄A的北偏东15°的方向上，已知PA平分∠BPN，AP＝2km，求村庄A，B之间的距离．（计算结果精确到0.01km，参考数据：≈1.414，≈1.732，≈2.449）

Answer 1

【答案】村庄A，B之间的距离约为2.23 km．

【解析】

延长AQ交MN于点D，则AD⊥MN，过点P作PC⊥AB于点C．根据题意可得，∠PAD＝15°．然后根据锐角三角函数即可求出村庄A，B之间的距离．

解：如图，延长AQ交MN于点D，

则AD⊥MN，过点P作PC⊥AB于点C．

根据题意可知：∠PAD＝15°，

∴∠APD＝90°﹣∠PAD＝75°，

∵AP平分∠BPN，

∴∠APD＝∠APB＝75°，

∵∠QAB＝60°，

∴∠PAB＝∠QAB﹣∠PAD＝45°，

∴∠PBA＝180°﹣∠PAB﹣∠APB＝60°，

在Rt△APC中，∠ACP＝90°，∠PAC＝45°，AP＝2，

∴，

即，

∴，

∴AC＝PC＝，

在Rt△PCB中，∠BCP＝90°，∠PBA＝60°，，

∴，

即，

∴，

∴≈1.414+≈2.23（km）．

答：村庄A，B之间的距离约为2.23 km．