Question

【题目】如图所示，在平面直角坐标系中，抛物线y=－x2＋2x的顶点为A点，且与x轴的正半轴交于点B，P点为该抛物线对称轴上一点，则OP＋AP的最小值为（ ）.

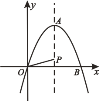
A. 3 B. C. D.

Answer 1

【答案】A

【解析】

连接AO,AB,PB,作PH⊥OA于H,BC⊥AO于C,解方程得到－x2＋2x=0得到点B,再利用配方法得到点A，得到OA的长度，判断△AOB为等边三角形，然后利用∠OAP=30°得到PH= AP,利用抛物线的性质得到PO=PB,再根据两点之间线段最短求解.

连接AO,AB,PB,作PH⊥OA于H,BC⊥AO于C,如图当y=0时－x2＋2x=0，得x1=0,x2=2,所以B（2,0），由于y=－x2＋2x=-(x-)2+3,所以A（,3）,所以AB=AO=2,AO=AB=OB，所以三角形AOB为等边三角形，∠OAP=30°得到PH= AP,因为AP垂直平分OB,所以PO=PB，所以OP＋AP=PB+PH，所以当H,P,B共线时，PB+PH最短，而BC=AB=3，所以最小值为3.

故选A.