题目内容
当x 时,式子
在实数范围内有意义;若(a+2)2+|b-1|+
=0,则a+b+c= .
| 5+2x |
| 3-c |
考点:非负数的性质:算术平方根,非负数的性质:绝对值,非负数的性质:偶次方,二次根式有意义的条件
专题:
分析:根据被开方数≥0,即可得出x的范围;
根据非负数的性质列出方程求出x、y的值,代入所求代数式计算即可.
根据非负数的性质列出方程求出x、y的值,代入所求代数式计算即可.
解答:解:∵5+2x≥0,
∴x≥-2.5;
∵(a+2)2+|b-1|+
=0,
∴
,
解得a=-2,b=1,c=3,
∴a+b+c=-2+1+3=2.
∴x≥-2.5;
∵(a+2)2+|b-1|+
| 3-c |
∴
|
解得a=-2,b=1,c=3,
∴a+b+c=-2+1+3=2.
点评:本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
如果a的倒数是-1,那么a201等于( )
| A、1 | B、-1 |
| C、201 | D、-201 |
若(a-1)2+|b+2|=0,则(a+b)2014的值是( )
| A、-1 | B、1 | C、0 | D、2014 |
下列计算正确的是( )
A、
| ||||||||||||||
B、
| ||||||||||||||
C、
| ||||||||||||||
D、
|
 如图,已知∠AOB=60°,点P在∠AOB内,OP=6cm,E、F为OA、OB上的点,要使△PEF的周长最小,请在图中画出E、F的位置,并求出△PEF周长的最小值.
如图,已知∠AOB=60°,点P在∠AOB内,OP=6cm,E、F为OA、OB上的点,要使△PEF的周长最小,请在图中画出E、F的位置,并求出△PEF周长的最小值.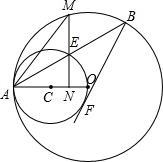 如图,OA是⊙O的半径,以OA为直径的⊙C与⊙O的弦AB交于点E.
如图,OA是⊙O的半径,以OA为直径的⊙C与⊙O的弦AB交于点E.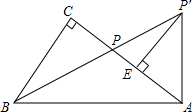 如图,在Rt△ABC中,∠C=90°,AP′⊥AB,BP′交AC于点P,AP=AP′.
如图,在Rt△ABC中,∠C=90°,AP′⊥AB,BP′交AC于点P,AP=AP′.