题目内容
 如图,已知∠AOB=60°,点P在∠AOB内,OP=6cm,E、F为OA、OB上的点,要使△PEF的周长最小,请在图中画出E、F的位置,并求出△PEF周长的最小值.
如图,已知∠AOB=60°,点P在∠AOB内,OP=6cm,E、F为OA、OB上的点,要使△PEF的周长最小,请在图中画出E、F的位置,并求出△PEF周长的最小值.考点:轴对称-最短路线问题
专题:
分析:作P关于OA的对称点,以及关于OB的对称点,连接两个对称点,交OA、OB分别于E、F,则此时△PEF的周长最小,进而求出△PEF的周长.
解答: 解:如图所示:E、F即为所求,此时△PEF周长最小,
解:如图所示:E、F即为所求,此时△PEF周长最小,
过点O作OM⊥P′P″于点M,
∵∠AOB=60°,P关于OA的对称点P′,P关于OB的对称点P″,
∴OP′=OP=OP″=6cm,∠P′OP″=120°,
∴∠OP′P″=∠OP″P′=30°,
∴P′M=OP′cos30°=3
cm,
则P′P″=6
cm,
即△PEF周长的最小值为6
cm.
 解:如图所示:E、F即为所求,此时△PEF周长最小,
解:如图所示:E、F即为所求,此时△PEF周长最小,过点O作OM⊥P′P″于点M,
∵∠AOB=60°,P关于OA的对称点P′,P关于OB的对称点P″,
∴OP′=OP=OP″=6cm,∠P′OP″=120°,
∴∠OP′P″=∠OP″P′=30°,
∴P′M=OP′cos30°=3
| 3 |
则P′P″=6
| 3 |
即△PEF周长的最小值为6
| 3 |
点评:此题主要考查了轴对称最短路径问题,关键是确定E,F的位置,然后找到最小周长的三角形,然后求出最小周长.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
若直角三角形的三边长分别为5,12,x,则x2的值为( )
| A、169 | B、119 |
| C、169或119 | D、196或13 |
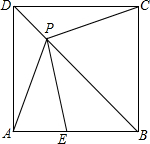 已知:如图,正方形ABCD的边长为6
已知:如图,正方形ABCD的边长为6