题目内容
6.已知二次函数y=2x2+8x-1,则它的顶点为(-2,-9),将这个二次函数向上平移2个单位长度,再向右平移2个单位长度后得到新的函数表达式为y=2(x+2)2-7.分析 先利用配方法得到二次函数y=2x2+8x-1的图象的顶点坐标为(-2,-9),再根据点平移的规律得到点(-2,-9)经过平移后所得对应点的坐标为(-2,-7),然后根据顶点式写出平移后的二次函数图象的解析式.
解答 解:∵y=2x2+8x-1=2(x+2)2-9,
∴二次函数y=2x2+8x-1的图象的顶点坐标为(-2,-9),
∵点(-2,-9)向上平移2个单位后所得对应点的坐标为(-2,-7),
∴平移后的二次函数图象的解析式为y=2(x+2)2-7.
故答案为(-2,-9),y=2(x+2)2-7.
点评 本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
相关题目
16.下列各组中的两项是同类项的是( )
| A. | 16zy2和-12y2z | B. | -m2n和mn2 | C. | -x2和3x | D. | 0.5a和0.5b |
18.下列各组线段中,成比例的是( )
| A. | a=3 cm,b=5 cm,c=14 cm,d=8cm | B. | a=6 cm,b=8 cm,c=3 cm,d=4cm | ||
| C. | a=3 cm,b=5 cm,c=9 cm,d=12cm | D. | a=2 cm,b=3 cm,c=6cm,d=12cm |
16.设a=2°,b=(-3)2,c=$\root{3}{27}$,d=($\frac{1}{2}$) -1,则a、b、c、d按由小到大的顺序排列正确的是( )
| A. | a<d<c<b | B. | a<b<c<d | C. | d<a<c<b | D. | b<d<c<a |
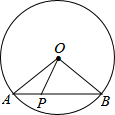 如图,⊙O的半径是2,AB是⊙O的弦,点P是弦AB上的动点,且1≤OP≤2,则弦AB所对的圆周角的度数是60°或120°.
如图,⊙O的半径是2,AB是⊙O的弦,点P是弦AB上的动点,且1≤OP≤2,则弦AB所对的圆周角的度数是60°或120°.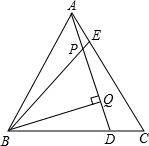 如图,在等边三角形ABC中,AE=CD,AD、BE交于Q点,BP⊥AD于P点.
如图,在等边三角形ABC中,AE=CD,AD、BE交于Q点,BP⊥AD于P点.