题目内容
1.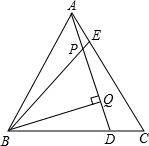 如图,在等边三角形ABC中,AE=CD,AD、BE交于Q点,BP⊥AD于P点.
如图,在等边三角形ABC中,AE=CD,AD、BE交于Q点,BP⊥AD于P点.求证:(1)△BAE≌△ACD;
(2)∠BQP=60°;
(3)BQ=2PQ.
分析 (1)由AB=AC,∠BAE=∠C,AE=CD,即可证明.
(2)根据三角形的外角的性质,∠BPQ=∠2+∠3=∠1+∠3=∠BAC=60°,即可证明.
(3)利用直角三角形30度性质即可解决问题.
解答 (1)证明:∵△ABC是等边三角形,
∴AB=AC,∠BAE=∠C=60°,
在△ABE和△CAD中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAE=∠C=60°}\\{AE=CD}\end{array}\right.$,
∴△ABE≌△CAD(SAS),
(2)∵△ABE≌△CAD
∴∠1=∠2,
∴∠BPQ=∠2+∠3=∠1+∠3=∠BAC=60°,
(3)∵BQ⊥AD,
∴∠PBQ=90°-∠BPQ=90°-60°=30°,
∴BP=2PQ.
点评 此题考查了全等三角形的判定与性质,等边三角形的性质,直角三角形30°角所对的直角边等于斜边的一半的性质,熟记各性质并准确识图求出△BPQ是含30°角的直角三角形是解题的关键.

练习册系列答案
相关题目
12.把一条弯曲的河道改成直道,可以缩短航程,其中的道理可以解释为( )
| A. | 线段有两个端点 | B. | 两点之间,直线最短 | ||
| C. | 两点之间,线段最短 | D. | 线段可以比较大小 |
9.下列计算正确的是( )
| A. | 23=6 | B. | -4-16=-20 | C. | -8-8=0 | D. | -5-2=-3 |
 如图,正方形网格中的每个小正方形边长都是1,每个小格顶点为格点,以格点为顶点分别按下列要求画图.
如图,正方形网格中的每个小正方形边长都是1,每个小格顶点为格点,以格点为顶点分别按下列要求画图. 已知某市2015年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.
已知某市2015年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图. (1)在数轴上表示下列各数,
(1)在数轴上表示下列各数,