题目内容
5. 如图,在等腰△ABC中,AB=AC,∠BAC=120°,腰AB的垂直平分线交底BC于点D,垂足为点E.
如图,在等腰△ABC中,AB=AC,∠BAC=120°,腰AB的垂直平分线交底BC于点D,垂足为点E.(1)求∠BAD的度数;
(2)若DB=2cm,求CB的长.
分析 (1)根据三角形内角和定理和等腰三角形的性质求出∠B=∠C=30°,根据垂直平分线的性质解答即可;
(2)根据直角三角形中,30°角所对的直角边等于斜边的一半计算.
解答 解:(1)∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵DE是AB的垂直平分线,
∴∠BAD=∠B=30°;
(2)∵∠BAC=120°,∠BAD=30°,
∴∠CAD=90°,又∠C=30°,
∴CD=2AD=4,
∴BC=CD+DB=6cm.
点评 本题考查的是线段的垂直平分线的性质,掌握垂直平分线上任意一点,到线段两端点的距离相等是解题的关键.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
15.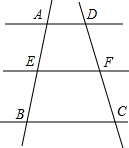 如图,AD∥EF∥BC,下列选项不成立的是( )
如图,AD∥EF∥BC,下列选项不成立的是( )
 如图,AD∥EF∥BC,下列选项不成立的是( )
如图,AD∥EF∥BC,下列选项不成立的是( )| A. | $\frac{AE}{EB}$=$\frac{DF}{FC}$ | B. | $\frac{BE}{CF}$=$\frac{AE}{DF}$ | C. | $\frac{AE}{AB}$=$\frac{AD}{BC}$ | D. | $\frac{AE}{DF}$=$\frac{AB}{DC}$ |
 如图所示,将面积为5的△ABC沿BC方向平移至△DEF的位置,平移的距离是边BC长的两倍,那么图中的四边形ACED的面积为( )
如图所示,将面积为5的△ABC沿BC方向平移至△DEF的位置,平移的距离是边BC长的两倍,那么图中的四边形ACED的面积为( ) 如图,在直角坐标系中,⊙P沿着x轴,绕它的圆心P向原点方向滚动,当⊙P旋转2周时,⊙P与y轴相交于点(0,2)和(0,8),则⊙P开始滚动时圆心的坐标是(40π+4,5).
如图,在直角坐标系中,⊙P沿着x轴,绕它的圆心P向原点方向滚动,当⊙P旋转2周时,⊙P与y轴相交于点(0,2)和(0,8),则⊙P开始滚动时圆心的坐标是(40π+4,5).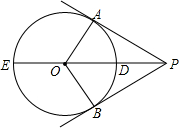 如图所示,PA,PB是⊙O的两条切线,A,B为切点,直线OP交⊙O于点D,E.
如图所示,PA,PB是⊙O的两条切线,A,B为切点,直线OP交⊙O于点D,E.