题目内容
15. 如图所示,将面积为5的△ABC沿BC方向平移至△DEF的位置,平移的距离是边BC长的两倍,那么图中的四边形ACED的面积为( )
如图所示,将面积为5的△ABC沿BC方向平移至△DEF的位置,平移的距离是边BC长的两倍,那么图中的四边形ACED的面积为( )| A. | 10 | B. | 15 | C. | 20 | D. | 25 |
分析 设点A到BC的距离为h,根据平移的性质用BC表示出AD、CE,然后根据三角形的面积公式与梯形的面积公式列式进行计算即可得解.
解答 解:设点A到BC的距离为h,则S△ABC=$\frac{1}{2}$BC•h=5,
∵平移的距离是BC的长的2倍,
∴AD=2BC,CE=BC,
∴四边形ACED的面积=$\frac{1}{2}$(AD+CE)•h=$\frac{1}{2}$(2BC+BC)•h=3×$\frac{1}{2}$BC•h=3×5=15.
故选B
点评 本题考查了平移的性质,三角形的面积,主要用了对应点间的距离等于平移的距离的性质.

练习册系列答案
 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
10.若a<0,则点M(-a,a)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
20.下列函数中,y随x的增大而减小的是( )
| A. | y=x | B. | y=x2 | C. | y=$\frac{2}{x}$ | D. | y=$\frac{4}{x}$(x<0) |
7. 如图,在圆内接四边形ABCD中,∠B=50°,则∠D=( )
如图,在圆内接四边形ABCD中,∠B=50°,则∠D=( )
 如图,在圆内接四边形ABCD中,∠B=50°,则∠D=( )
如图,在圆内接四边形ABCD中,∠B=50°,则∠D=( )| A. | 40° | B. | 130° | C. | 120° | D. | 150° |
4.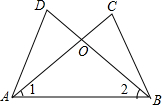 如图,已知∠1=∠2,若用“SAS”来判定△ACB≌△BDA,则还需要添加的一个条件是( )
如图,已知∠1=∠2,若用“SAS”来判定△ACB≌△BDA,则还需要添加的一个条件是( )
 如图,已知∠1=∠2,若用“SAS”来判定△ACB≌△BDA,则还需要添加的一个条件是( )
如图,已知∠1=∠2,若用“SAS”来判定△ACB≌△BDA,则还需要添加的一个条件是( )| A. | AD=BC | B. | AC=BD | C. | ∠C=∠D | D. | OA=OB |
 如图,在长方形纸片ABCD中,AB=6cm,BC=10cm,将长方形纸片沿AE折叠,使点D落在BC边的点F处.试求折痕AE的长.
如图,在长方形纸片ABCD中,AB=6cm,BC=10cm,将长方形纸片沿AE折叠,使点D落在BC边的点F处.试求折痕AE的长. 如图,在等腰△ABC中,AB=AC,∠BAC=120°,腰AB的垂直平分线交底BC于点D,垂足为点E.
如图,在等腰△ABC中,AB=AC,∠BAC=120°,腰AB的垂直平分线交底BC于点D,垂足为点E.