Question

12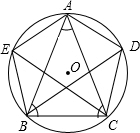．如图，在⊙O的内接等腰三角形ABC中，AB=AC，弦BD、CE分别平分∠ABC、∠ACB，BE=BC．
（1）求证：五边形AEBCD是正五边形；
（2）若BD、CE相交于点F，试判断四边形AEFD的形状，并证明你的结论．

Answer 1

分析 （1）欲求证五边形AEBCD是正五边形，就是证明这个五边形的五条边所对的弧相等即可；
（2）首先利用正五边形的性质得出AE∥BD，同理可得：EC∥AD，进而利用菱形的判定方法得出答案．

解答 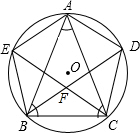（1）证明：∵AB=AC，
∴∠ABC=∠ACB，
∵弦BD，CE分别平分∠ABC，∠ACB，
∴∠ABD=∠DBC=∠ECB=∠ACE，
∵BE=BC，
∴$\widehat{BE}$=$\widehat{BC}$，
∴∠BEC=∠BCE，
∵∠BCA=∠BEC，
∴∠ABD=∠DBC=∠ECB=∠ACE=∠BAC，
∴$\widehat{AE}$=$\widehat{AD}$=$\widehat{DC}$=$\widehat{BC}$=$\widehat{BE}$，
∴五边形AEBCD是正五边形；

（2）四边形AEFD是菱形，
理由：∵五边形AEBCD是正五边形，
∴∠EBC=∠EAD=∠AEB=∠ADC=∠BCD=108°，
∵BC=DC，
∴∠CBD=∠BDC=36°，
∴∠ADB=72°，
∴∠EAD+∠ADB=180°，
∴AE∥BD，
同理可得：EC∥AD，
则四边形AEFD是平行四边形，
∵AE=AD，
∴四边形AEFD是菱形．

点评 此题主要考查了正多边形和圆以及菱形的判定，正确掌握正多边形的性质与判定方法是解题关键．