题目内容
4.如图1,抛物线y=-$\frac{1}{2}$x2+bx+c与x轴交于点A(4,0)和点B(-1,0),与y轴交干点C,连结BC,CE∥x轴交抛物线于点E.(1)求抛物线的解析式.
(2)抛物线对称轴交x轴于点F,连结CF,EF,直线y=kx(x>0)与直线CA交于点D,当OD平分△BCA的面积时,求证:点D是△CEF的内心
(3)如图2,过点E作ER⊥x轴于点R,G是线段OR上动点,作ES⊥CG于点S.
①当△ESR是等腰三角形时,求OC的长.
②若点B1与点B关于直线CG对称,当EB1的值最小时,直接写出OG的值.
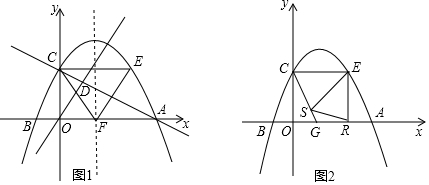
分析 (1)由抛物线y=-$\frac{1}{2}$x2+bx+c与x轴交于点A(4,0)和点B(-1,0),可知抛物线的解析式为y=-$\frac{1}{2}$(x-4)(x+1),写成一般式即可.
(2)首先求出点D的坐标,只要证明DF平分∠CFE,CD平分∠ECF即可.
(3)①分三种情形,想办法列出方程即可解决问题.②如图由题意,动点B′在以C为圆心$\sqrt{5}$为半径的⊙C上,易知当B′在线段CE上时,EB′最小.此时∠ECG=∠CGB=∠BCG,推出BC=BG,推出OG=BC-OB=$\sqrt{5}$-1.
解答 (1)解:∵抛物线y=-$\frac{1}{2}$x2+bx+c与x轴交于点A(4,0)和点B(-1,0),
∴抛物线的解析式为y=-$\frac{1}{2}$(x-4)(x+1)=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2.
(2)证明:如图1中,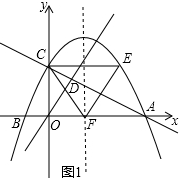
∵A(4,0),B(-1,0),C(0,2),
∴OB=1,OA=4,OC=2,
∴直线AC的解析式为y=-$\frac{1}{2}$x+2,设D(m,-$\frac{1}{2}$m+2),
∴S△ABC=$\frac{1}{2}$×5×2=5,
由题意S△AOD=$\frac{1}{2}$S△ABC,
∴$\frac{1}{2}$×4×(-$\frac{1}{2}$m+2)=$\frac{5}{2}$,
∴m=$\frac{3}{2}$,
∴D($\frac{3}{2}$,$\frac{5}{4}$),
∵抛物线的对称轴x=$\frac{3}{2}$,
∴点D在对称轴上,DF平分∠CFE,
在Rt△COF中,CF=$\sqrt{{2}^{2}+(\frac{3}{2})^{2}}$=$\frac{5}{2}$,∵AF=$\frac{5}{2}$,
∴CF=AF,
∴∠FAC=∠FCA,
∵CE∥OA,
∴∠ECA=∠CAF=∠ACF,
∴CD平分∠ECF,
∴点D是△ECF的内心.
(3)①如图2中,设G(m,0),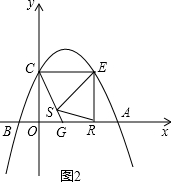
当ES=ER时,由△OCG∽△SEC,
∴$\frac{OC}{SE}$=$\frac{OG}{CS}$,
在Rt△CES中,CS=$\sqrt{C{E}^{2}-E{S}^{2}}$=$\sqrt{{3}^{2}-{2}^{2}}$=$\sqrt{5}$,
∴$\frac{2}{2}$=$\frac{m}{\sqrt{5}}$,
∴m=$\sqrt{5}$,
∴OG=$\sqrt{5}$.
当SE=ER时,如图3中,作SN⊥ER于N,则EN=NR=1,S($\frac{1}{2}$m,1),SN=3-$\frac{m}{2}$,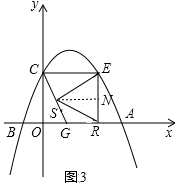
由△OCG∽△NSE,可得$\frac{OG}{EN}$=$\frac{OC}{SN}$,
∴$\frac{m}{1}$=$\frac{2}{3-\frac{m}{2}}$,
解得m=3-$\sqrt{5}$或3+$\sqrt{5}$(舍弃),
∴OG=3-$\sqrt{5}$.
当RE=RS时,如图4中,作RN⊥SE于N,GM⊥RN于M.则SN=EN=GM,设SN=EN=GM=x,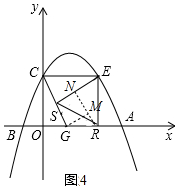
由△OCG∽△MGR,可得$\frac{CG}{GR}$=$\frac{OC}{GM}$,
∴$\frac{\sqrt{4+{m}^{2}}}{3-m}$=$\frac{2}{x}$,
∴x=$\frac{2(3-m)}{\sqrt{4+{m}^{2}}}$,
∴SN=EN=GM=$\frac{2(3-m)}{\sqrt{4+{m}^{2}}}$,
由△OCG∽△NRE,可得$\frac{OG}{EN}$=$\frac{CG}{ER}$,
∴$\frac{m}{\frac{2(3-m)}{\sqrt{4+{m}^{2}}}}$=$\frac{\sqrt{4+{m}^{2}}}{2}$,
解得m=$\frac{3}{2}$,
∴OG=$\frac{3}{2}$,
综上所述,当△ESR是等腰三角形时,OG的长为$\sqrt{5}$或3-$\sqrt{5}$或$\frac{3}{2}$.
②如图5中,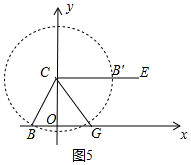
如图由题意,动点B′在以C为圆心$\sqrt{5}$为半径的⊙C上,易知当B′在线段CE上时,EB′最小.
此时∠ECG=∠CGB=∠BCG,
∴BC=BG,
∴OG=BC-OB=$\sqrt{5}$-1.
点评 本题考查二次函数综合题、待定系数法、等腰三角形的判定和性质、圆的有关知识、勾股定理、三角形的内心、一元二次方程等知识,解题的关键是灵活运用所学知识,学会用分类讨论的思想思考问题,学会利用参数,构建方程解决问题,属于中考压轴题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | -1 | B. | 1 | C. | ±1 | D. | 不能确定 |
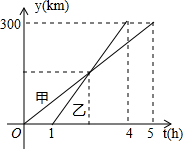 如图,甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A成的距离y(千米)与甲车行驶的时间t(时)之间的关系如图所示,观察图象回答下列问题:
如图,甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A成的距离y(千米)与甲车行驶的时间t(时)之间的关系如图所示,观察图象回答下列问题: 一次函数y=kx+b(k,b为常数,k≠0)的图象如图所示,根据图象信息可求得关于x的方程kx+b=3的解为x=2.
一次函数y=kx+b(k,b为常数,k≠0)的图象如图所示,根据图象信息可求得关于x的方程kx+b=3的解为x=2.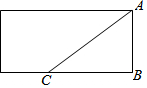 如图,在一个长方形的木块上截下一个三角形ABC,使AB=6cm,BC=8cm,截线AC的长是多少?
如图,在一个长方形的木块上截下一个三角形ABC,使AB=6cm,BC=8cm,截线AC的长是多少?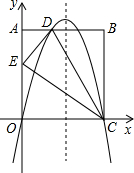 如图,在矩形ABCD中,AO=10,AB=8,分别以OC、OA所在的直线为x轴,y轴建立平面直角坐标系,点D(3,10)、E(0,6),抛物线y=ax2+bx+c经过O,D,C三点.
如图,在矩形ABCD中,AO=10,AB=8,分别以OC、OA所在的直线为x轴,y轴建立平面直角坐标系,点D(3,10)、E(0,6),抛物线y=ax2+bx+c经过O,D,C三点.