Question

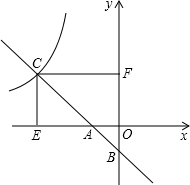如图，一次函数y₁=mx+n的图象与x轴、y轴分别交于A、B两点，与反比例函数y₂=

k

x

（x＜0）交于点C，过点C分别作x轴、y轴的垂线，垂足分别为点E、F．若OB=2，CF=6，

OA

OE

=

1

3

．
（1）求点A的坐标；
（2）求一次函数和反比例函数的表达式．

Answer 1

考点：反比例函数与一次函数的交点问题

专题：计算题

分析：（1）利用

OA

OE

=

1

3

，OE=CF=6，可计算出OA=2，于是得到A点坐标为（-2，0）；
（2）由于B点坐标为（0，-2），则可利用待定系数法求出一次函数解析式为y₁=-x-2，再利用一次函数解析式确定C点坐标为（-6，4），根据反比例函数图象上点的坐标特征计算出k=-24，所以反比例函数解析式为y₂=-

24

x

．

解答：解：（1）∵

OA

OE

=

1

3

，
而OE=CF=6，
∴OA=2，
∴A点坐标为（-2，0）；
（2）B点坐标为（0，-2），
把A（-2，0）、B（0，-2）代入y₁=mx+n得

-2k+b=0 b=-2

，即得

k=-1 b=-2

，
∴一次函数解析式为y₁=-x-2；
把x=-6代入y₁=-x-2得y=6-2=4，
∴C点坐标为（-6，4），
∴k=-6×4=-24，
∴反比例函数解析式为y₂=-

24

x

．

点评：本题考查了反比例函数与一次函数的交点问题：反比例函数与一次函数图象的交点坐标满足两函数解析式．也考查了待定系数法求函数解析式以及观察函数图象的能力．