题目内容
分解因式:
(1)x2-6x-7
(2)x2+6x-7
(3)x2-8x+7
(4)x2+8x+7
(5)x2-5x+6
(6)x2-5x-6
(7)x2+5x-6
(8)x2+5x+6.
(1)x2-6x-7
(2)x2+6x-7
(3)x2-8x+7
(4)x2+8x+7
(5)x2-5x+6
(6)x2-5x-6
(7)x2+5x-6
(8)x2+5x+6.
考点:因式分解-十字相乘法等
专题:
分析:(1)x2+(p+q)x+pq型的式子的因式分解,这类二次三项式的特点是:二次项的系数是1;常数项是两个数的积;
可以直接将某些二次项的系数是1的二次三项式因式分解:x2+(p+q)x+pq=(x+p)(x+q);
(2)利用十字相乘法直接分解因式即可;
(3)利用十字相乘法直接分解因式即可;
(4)利用十字相乘法直接分解因式即可;
(5)利用十字相乘法直接分解因式即可;
(6)利用十字相乘法直接分解因式即可;
(7)利用十字相乘法直接分解因式即可;
(8)利用十字相乘法直接分解因式即可.
可以直接将某些二次项的系数是1的二次三项式因式分解:x2+(p+q)x+pq=(x+p)(x+q);
(2)利用十字相乘法直接分解因式即可;
(3)利用十字相乘法直接分解因式即可;
(4)利用十字相乘法直接分解因式即可;
(5)利用十字相乘法直接分解因式即可;
(6)利用十字相乘法直接分解因式即可;
(7)利用十字相乘法直接分解因式即可;
(8)利用十字相乘法直接分解因式即可.
解答:解:(1)x2-6x-7=(x-7)(x+1);
(2)x2+6x-7=(x+7)(x11);
(3)x2-8x+7=(x-7)(x-1);
(4)x2+8x+7=(x+7)(x+1);
(5)x2-5x+6=(x-3)(x-2);
(6)x2-5x-6=(x-6)(x+1);
(7)x2+5x-6=(x+6)(x-1);
(8)x2+5x+6=(x+2)(x+3).
(2)x2+6x-7=(x+7)(x11);
(3)x2-8x+7=(x-7)(x-1);
(4)x2+8x+7=(x+7)(x+1);
(5)x2-5x+6=(x-3)(x-2);
(6)x2-5x-6=(x-6)(x+1);
(7)x2+5x-6=(x+6)(x-1);
(8)x2+5x+6=(x+2)(x+3).
点评:此题主要考查了十字相乘法分解因式,正确分解常数项是解题关键.

练习册系列答案
相关题目
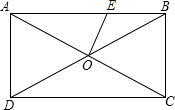 如图,矩形ABCD中,AC交BD于O,∠AOD=60°,OE⊥AC,AD=
如图,矩形ABCD中,AC交BD于O,∠AOD=60°,OE⊥AC,AD= 抛物线y=ax2-4ax+c交x轴于A、B两点,已知A(1,0),抛物线经过点N(4,-3),交y轴于点C.
抛物线y=ax2-4ax+c交x轴于A、B两点,已知A(1,0),抛物线经过点N(4,-3),交y轴于点C.