题目内容
一个整数与2的差的绝对值大于2012小于2014,则这个整数是 .
考点:有理数的减法,绝对值
专题:
分析:可以设这个整数是x,根据个整数与5之差的绝对值大于2012小于2014,即可列出不等式,即可求解.
解答:解:设这个整数是x,根据题意得:
2012<|x-2|<2014,
则2012<x-2<2014或-2014<x-2<-2012,
解得:2014<x<2016或-2012<x<-2014,
故这个整数是2015或-2013.
故答案是:2015或-2013.
2012<|x-2|<2014,
则2012<x-2<2014或-2014<x-2<-2012,
解得:2014<x<2016或-2012<x<-2014,
故这个整数是2015或-2013.
故答案是:2015或-2013.
点评:本题主要考查了不等式组的解法,注意各个不等式的解集的公式部分就是这个不等式组的解集.但本题是要求整数解的,所以要找出在这范围内的整数.

练习册系列答案
相关题目
一元二次不等式ax2+bx+2>0的解为-
<x<
,则a-b=( )
| 1 |
| 2 |
| 1 |
| 3 |
| A、10 | B、-14 |
| C、-10 | D、-8 |
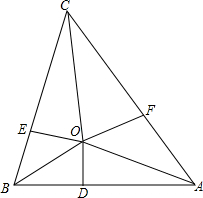 如图,已知在△ABC中,AO、BO、CO分别是∠BAC、∠ABC、∠ACB的角平分线,AB=4,BC=5,CA=6,OD⊥AB,OE⊥BC,OF⊥AC,求OD的长.
如图,已知在△ABC中,AO、BO、CO分别是∠BAC、∠ABC、∠ACB的角平分线,AB=4,BC=5,CA=6,OD⊥AB,OE⊥BC,OF⊥AC,求OD的长. 如图,△ABC中,D为AB中点,DE∥BC,若BC=16cm,则DE=
如图,△ABC中,D为AB中点,DE∥BC,若BC=16cm,则DE= 如图:AB长度为20厘米,AO=4厘米,PO=2厘米,∠POB=60°,点P绕着点O以60度/秒的速度逆时针旋转一周停止,同时点Q沿直线B自B点向A点运动,假若点P、Q两点能相遇,求点Q的运动速度.
如图:AB长度为20厘米,AO=4厘米,PO=2厘米,∠POB=60°,点P绕着点O以60度/秒的速度逆时针旋转一周停止,同时点Q沿直线B自B点向A点运动,假若点P、Q两点能相遇,求点Q的运动速度.