题目内容
9．已知抛物线y=ax2+bx+c（a＜0）过A（2$\sqrt{5}$，0）、O（0，0）、B（-3，y1）、C（3，y2）四点，则y1与y2的大小关系是（ ）| A． | y1＞y2 | B． | y1=y2 | C． | y1＜y2 | D． | 不能确定 |
分析 由已知可得抛物线与x轴交于A（2$\sqrt{5}$，0）、O（0，0）两点，开口向下，对称轴为x=$\sqrt{5}$，可知B、C两点在对称轴的两边，点B离对称轴较近，再根据抛物线图象进行判断．
解答 解：∵抛物线与x轴交于A（2$\sqrt{5}$，0）、O（0，0）两点，
∴抛物线对称轴为x=$\frac{2\sqrt{5}+0}{2}$=$\sqrt{5}$，
∵B（-3，y1）、C（3，y2），点C离对称轴较近，且抛物线开口向下，
∴y1＜y2．
故选C．
点评 本题考查了二次函数的增减性．当二次项系数a＞0时，在对称轴的左边，y随x的增大而减小，在对称轴的右边，y随x的增大而增大；a＜0时，在对称轴的左边，y随x的增大而增大，在对称轴的右边，y随x的增大而减小．
练习册系列答案
阅读快车系列答案
相关题目
19．某中学举行了一次演讲比赛，分段统计参赛同学的成绩，结果如下表（分数均为整数，满分为100分）：
根据表中提供的信息，回答下列问题：
①参加这次演讲比赛的同学共20人；
②成绩在91～100分的为优胜者，优胜率为20%．
| 分数段 | 61～70 | 71～80 | 81～90 | 91～100 |
| 人数（人） | 2 | 8 | 6 | 4 |
①参加这次演讲比赛的同学共20人；
②成绩在91～100分的为优胜者，优胜率为20%．
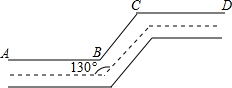如图，一条公路两次转完后又回到原来的方向（即AB∥CD），如果第一次转弯时的∠B=130°，那么第二次转弯时的∠C=130度．
14．在数轴上与原点的距离小于5的点对应的x满足（ ）
| A． | -5＜x＜5 | B． | x＜5 | C． | x＜-5或x＞5 | D． | x＞5 |
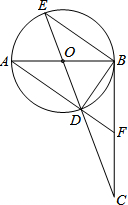如图，AB是⊙O的直径，BC⊥AB，垂足为点B，连接CO并延长交⊙O于点D、E，连接AD并延长交BC于点F．则下列结论正确的有（ ）