题目内容
18.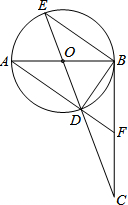 如图,AB是⊙O的直径,BC⊥AB,垂足为点B,连接CO并延长交⊙O于点D、E,连接AD并延长交BC于点F.则下列结论正确的有( )
如图,AB是⊙O的直径,BC⊥AB,垂足为点B,连接CO并延长交⊙O于点D、E,连接AD并延长交BC于点F.则下列结论正确的有( )①∠CBD=∠CEB;②$\frac{BD}{BE}$=$\frac{CD}{BC}$;③点F是BC的中点;④若$\frac{BC}{AB}$=$\frac{3}{2}$,tanE=$\frac{\sqrt{10}-1}{3}$.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ①正确,运用圆周角定理以及等角的余角相等即可解决问题.
②正确,运用△EBC∽△BDC即可证明.
③错误,运用反证法来判定.
④正确,设BC=3x,AB=2x,得出OB、OD及OC、CD的值,运用$\frac{BD}{BE}=\frac{CD}{BC}$即可解决问题.
解答 证明:(1)∵BC⊥AB于点B,
∴∠CBD+∠ABD=90°,
∵∠BAD+∠ABD=90°
∴∠CBD=∠BAD,
∵∠BAD=∠CEB,
∴∠CEB=∠CBD,
故①正确.
(2)∵∠C=∠C,∠CEB=∠CBD,
∴△EBC∽△BDC,
∴$\frac{BD}{BE}=\frac{CD}{BC}$,
故②正确,
(3)∵∠EBD=∠BDF=90°,
∴DF∥BE,
假设点F是BC的中点,则点D是EC的中点,
∴ED=DC,
∵ED是直径,长度不变,而DC的长度是不定的,
∴DC不一定等于ED,
故③是错误的.
(4)∵$\frac{BC}{AB}=\frac{3}{2}$,
设BC=3x,AB=2x,
∴OB=OD=x,
∴在RT△CBO中,OC=$\sqrt{10}$x,
∴CD=($\sqrt{10}$-1)x
∵由(2)知,$\frac{BD}{BE}=\frac{CD}{CB}$
∴$\frac{BD}{BE}=\frac{CD}{BC}$=$\frac{(\sqrt{10}-1)x}{3x}$=$\frac{\sqrt{10}-1}{3}$,
∵tanE=$\frac{BD}{BE}$
∴tanE=$\frac{\sqrt{10}-1}{3}$,
故④正确.
故选:C.
点评 本题主要考查了圆的综合题,涉及相似三角形的判定与性质、圆周角定理、锐角三角函数定义等知识点,解题的关键在于灵活应用这些知识解决问题,通过求证三角形相似根据对应边成比例的性质求出tan∠E的值,属于中考压轴题.

 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能确定 |
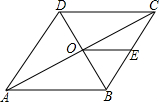 如图,在菱形ABCD中,对角线AC,BD相交于点O,点E为BC的中点,则下列等式中一定成立的是( )
如图,在菱形ABCD中,对角线AC,BD相交于点O,点E为BC的中点,则下列等式中一定成立的是( )| A. | AB=BE | B. | AC=2AB | C. | AB=2OE | D. | AC=2OE |
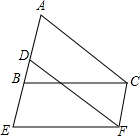 如图,将三角形ABC沿射线AB的方向平移2个单位到三角形DEF的位置,连接CF,点A,B,C的对应点分别是点D,E,F.
如图,将三角形ABC沿射线AB的方向平移2个单位到三角形DEF的位置,连接CF,点A,B,C的对应点分别是点D,E,F.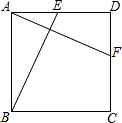 如图,在正方形ABCD中,点E,F分别在AD,CD上,且AE=DF,连接BE,AF.求证:BE=AF.
如图,在正方形ABCD中,点E,F分别在AD,CD上,且AE=DF,连接BE,AF.求证:BE=AF.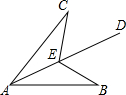 如图,AD平分∠BAC,点E在射线AD上,∠BED=∠CED,求证:AB=AC.
如图,AD平分∠BAC,点E在射线AD上,∠BED=∠CED,求证:AB=AC.