题目内容
如图，已知AB=AD，∠BAE=∠DAC，要使△ABC≌△ADE，只需增加一个条件是考点：全等三角形的判定
专题：开放型
分析：根据三角形全等的条件可得出AC=AE，∠C=∠E，∠B=∠D都可以．
解答：解：∵∠BAE=∠DAC，
∴∠BAE+∠CAE=∠DAC+∠CAE，
即∠BAC=∠DAE，
∵AB=AD，
∴添加AC=AE，根据SAS即可得证；
或添加∠C=∠E，根据AAS即可得证；
或添加∠B=∠D，根据ASA即可得证．
故答案为AC=AE或∠C=∠E或∠B=∠D．
∴∠BAE+∠CAE=∠DAC+∠CAE，
即∠BAC=∠DAE，
∵AB=AD，
∴添加AC=AE，根据SAS即可得证；
或添加∠C=∠E，根据AAS即可得证；
或添加∠B=∠D，根据ASA即可得证．
故答案为AC=AE或∠C=∠E或∠B=∠D．
点评：本题考查了全等三角形的判定，本题是个简单的开放型题目，要熟练掌握．
练习册系列答案
浙江名校名师金卷系列答案
全优冲刺100分系列答案
相关题目
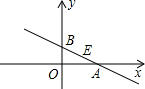如图，在平面直角坐标系xOy中，直线y=kx+b交x轴于点A，交y轴于点B，线段AB的中点E的坐标为（2，1）．
如图是叠放在一起的两张长方形卡片，则图中相等的角是（ ）| A、∠1与∠2 |
| B、∠2与∠3 |
| C、∠1与∠3 |
| D、三个角都相等 |