题目内容
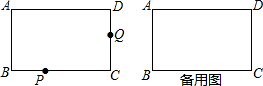
 如图是叠放在一起的两张长方形卡片,则图中相等的角是( )
如图是叠放在一起的两张长方形卡片,则图中相等的角是( )| A、∠1与∠2 |
| B、∠2与∠3 |
| C、∠1与∠3 |
| D、三个角都相等 |
考点:平行线的性质
专题:
分析:连接GH,根据直角三角形的性质可知∠CGE=∠DEF,∠AGH=∠BKH,再根据两角互补的性质即可得出结论.
解答: 解:∵两张长方形卡片叠在一起,
解:∵两张长方形卡片叠在一起,
∴∠C=∠D=∠A=∠B=∠AEF,
∵∠CEG+∠DEF=90°,∠CEG+∠CGE=90°,
∴∠CGE=∠DEF,
∵∠3+∠CGE=180°,∠1+∠DFE=180°,
∴∠1与∠3的大小无法判定;
∵∠AHG=∠BHK,∠AGH+∠AHG=90°,∠BHK+∠BKH=90°,
∴∠AGH=∠BKH,
∵∠3+∠AGH=180°,∠2+∠BKH=180°,
∴∠2=∠3.
故选B.
 解:∵两张长方形卡片叠在一起,
解:∵两张长方形卡片叠在一起,∴∠C=∠D=∠A=∠B=∠AEF,
∵∠CEG+∠DEF=90°,∠CEG+∠CGE=90°,
∴∠CGE=∠DEF,
∵∠3+∠CGE=180°,∠1+∠DFE=180°,
∴∠1与∠3的大小无法判定;
∵∠AHG=∠BHK,∠AGH+∠AHG=90°,∠BHK+∠BKH=90°,
∴∠AGH=∠BKH,
∵∠3+∠AGH=180°,∠2+∠BKH=180°,
∴∠2=∠3.
故选B.
点评:本题考查的是平行线的性质,熟知矩形的两边互相平行,且四个角均为直角是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,若∠A+∠B=180°,则有( )
如图,若∠A+∠B=180°,则有( )| A、∠B=∠C |
| B、∠A=∠ADC |
| C、∠1=∠B |
| D、∠1=∠C |
 如图,已知AB∥CD,∠1=115°,∠2=65°,则∠C等于( )
如图,已知AB∥CD,∠1=115°,∠2=65°,则∠C等于( )| A、40° | B、45° |
| C、50° | D、60° |
 如图,A是反比例函数y=
如图,A是反比例函数y=| k |
| x |
| A、-4 | B、1 | C、2 | D、4 |
甲校的女生占所有学生的50%,乙校的男生占所有学生的60%,那么( )
| A、甲校的女生人数多 |
| B、乙校的女生人数多 |
| C、两个学校的女生一样多 |
| D、不能判断 |
小明和小莉出生于2013年12月份,他们的出生日不是同一天,但都是星期五,且小明比小莉出生早,两人出生日期之和是33,那么小莉的出生日期是( )
| A、18号 | B、19号 |
| C、20号 | D、21号 |
 如图,已知AB=AD,∠BAE=∠DAC,要使△ABC≌△ADE,只需增加一个条件是
如图,已知AB=AD,∠BAE=∠DAC,要使△ABC≌△ADE,只需增加一个条件是