题目内容
13.已知$\frac{x}{y+z+t}$=$\frac{y}{z+t+x}$=$\frac{z}{t+x+y}$=$\frac{t}{x+y+z}$,记A=$\frac{x+y}{z+t}$+$\frac{y+z}{x+t}$+$\frac{z+t}{x+y}$+$\frac{t+x}{y+z}$,证明:A是一个整数.分析 分两种情况进行计算,①用等比的性质找出x+y=-(z+t),x+t=-(y+z),代入A即可,②用等比的性质找出x+y=z+t,x+t=y+z,代入A即可,
解答 证明:设$\frac{x}{y+z+t}$=$\frac{y}{z+t+x}$=$\frac{z}{t+x+y}$=$\frac{t}{x+y+z}$=k,
①当x+y+z+t=0时,则有x+y+z=-t,
∴k=$\frac{y}{z+t+x}$=$\frac{t}{x+y+z}$=-1,
∴x+y=-(z+t),x+t=-(y+z),
∴A=$\frac{x+y}{z+t}$+$\frac{y+z}{x+t}$+$\frac{z+t}{x+y}$+$\frac{t+x}{y+z}$
=$\frac{-(z+t)}{z+t}$+$\frac{-(x+t)}{x+t}$+$\frac{-(x+y)}{x+y}$+$\frac{-(y+z)}{y+z}$
=-1+(-1)+(-1)+(-1)
=-4
∴A是一个整数.
②当x+y+z+t≠0时,
∵$\frac{x}{y+z+t}$=$\frac{y}{z+t+x}$=$\frac{z}{t+x+y}$=$\frac{t}{x+y+z}$=k,
∴k=$\frac{x+y+z+t}{3(x+y+z+t)}$=$\frac{1}{3}$,
∵$\frac{x}{y+z+t}$=$\frac{y}{z+t+x}$=k=$\frac{1}{3}$,
∴$\frac{x+y}{(x+z)+(x+y)}$=$\frac{1}{3}$,
∴x+y=z+t,
∵$\frac{y}{z+t+x}$=$\frac{z}{t+x+y}$=k=$\frac{1}{3}$,
∴y+z=x+t,
∴A=$\frac{x+y}{z+t}$+$\frac{y+z}{x+t}$+$\frac{z+t}{x+y}$+$\frac{t+x}{y+z}$
=$\frac{z+t}{z+t}$+$\frac{x+t}{x+t}$+$\frac{x+y}{x+y}$+$\frac{y+z}{y+z}$
=1+1+1+1
=4,
∴A是一个整数.
即:A是一个整数.
点评 此题是分式的等式的性质,主要考查了等比的性质,分式的化简,解本题的关键是熟练等比的性质,难点是分两种情况讨论计算.

| A. | 调查宇宙飞船“神舟九号”的零部件 | B. | 调查一批飞行员的视力 | ||
| C. | 调查八年级(下)语文书的排版正确率 | D. | 调查市民对“闯红灯”的认识状况 |
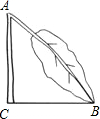 一棵树因雪灾于A处折断,如图所示,测得树梢触地点B到树根C处的距离为4米,∠ABC约45°,树干AC垂直于地面,那么此树在未折断之前的高度约为(4+4$\sqrt{2}$)米(答案可保留根号)
一棵树因雪灾于A处折断,如图所示,测得树梢触地点B到树根C处的距离为4米,∠ABC约45°,树干AC垂直于地面,那么此树在未折断之前的高度约为(4+4$\sqrt{2}$)米(答案可保留根号) 搭一搭,算一算;
搭一搭,算一算; 如图是一套住房的平面图,尺寸如图所.
如图是一套住房的平面图,尺寸如图所. 如图大正方形的面积为a2(a>0),小正方形的面积为b2(b>0),求阴影部分的面积.
如图大正方形的面积为a2(a>0),小正方形的面积为b2(b>0),求阴影部分的面积.