题目内容
若|a|=7,|b|=2,则|a+b|= .
考点:绝对值
专题:分类讨论
分析:根据绝对值的性质求出a、b,然后分情况代入计算即可得解.
解答:解:∵|a|=7,|b|=2,
∴a=±7,b=±2,
∴|a+b|=|7+2|=9,
|a+b|=|7-2|=5,
|a+b|=|-7+2|=5,
|a+b|=|-7-2|=9,
综上所述,|a+b|=5或9.
故答案为:5或9.
∴a=±7,b=±2,
∴|a+b|=|7+2|=9,
|a+b|=|7-2|=5,
|a+b|=|-7+2|=5,
|a+b|=|-7-2|=9,
综上所述,|a+b|=5或9.
故答案为:5或9.
点评:本题考查了绝对值,熟记性质是解题的关键,难点在于分情况讨论.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
某校2013年给希望工程捐款2万元,以后每年都捐款,计划到2015年三年总共捐款6.62万元,若设该校捐款的年平均增长率为x,则可列方程为( )
| A、2+2x2(1+x)=6.62 |
| B、2(1+x)2=6.62 |
| C、2+2(1+x)+2(1+x)2=6.62 |
| D、2(1+x)3=6.62 |
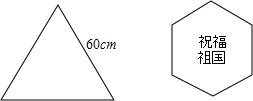 王明想用一块边长为60cm的等边三角形做成一个最大的正六边形,写上“祝福祖国”的字样来表达自己的喜悦之情,如图此六边形的边长是( )
王明想用一块边长为60cm的等边三角形做成一个最大的正六边形,写上“祝福祖国”的字样来表达自己的喜悦之情,如图此六边形的边长是( )| A、20cm | B、25cm |
| C、30cm | D、40cm |
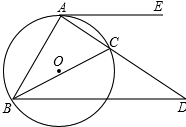 △ABC内接于⊙O,AE切⊙O于A,过B作BD平行AE交AC延长线于D,若AC=4cm CD=3cm,求AB的长.
△ABC内接于⊙O,AE切⊙O于A,过B作BD平行AE交AC延长线于D,若AC=4cm CD=3cm,求AB的长. 如图,圆内接正五边形ABCDE的半径为2,连接AC、BD相交于点F.
如图,圆内接正五边形ABCDE的半径为2,连接AC、BD相交于点F.
 如图,图中共有线段
如图,图中共有线段 如图,BM、CN是△ABC的角平分线,AE⊥BM于E,AF⊥CN于F.求证:EF∥BC.
如图,BM、CN是△ABC的角平分线,AE⊥BM于E,AF⊥CN于F.求证:EF∥BC.