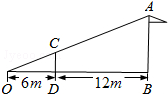如图.小明用长为3m的竹竿CD做测量工具.测量学校旗杆AB的高度.移动竹竿.使竹竿与旗杆的距离DB=12m.则旗杆AB的高为( )A．7mB．8mC．6mD．9m 题目和参考答案——青夏教育精英家教网—

题目内容

19．

如图，小明用长为3m的竹竿CD做测量工具，测量学校旗杆AB的高度，移动竹竿，使竹竿与旗杆的距离DB=12m，则旗杆AB的高为（　　）

A．

B．

C．

D．

分析先证明△OCD∽△OAB，则根据相似三角形的性质得到$\frac{3}{AB}$=$\frac{6}{6+12}$，然后利用比例的性质求AB即可．

解答解：∵CD∥AB，
∴△OCD∽△OAB，
∴$\frac{CD}{AB}$=$\frac{OD}{OB}$，即$\frac{3}{AB}$=$\frac{6}{6+12}$，
∴AB=9，
即旗杆AB的高为9m．
故选D．

点评本题考查了相似三角形的应用：利用视点和盲区的知识构建相似三角形，用相似三角形对应边的比相等的性质求物体的高度．

练习册系列答案

相关题目

9．直角三角形斜边上的中线与连结两直角边中点的线段的关系是（　　）

10．【发现问题】如图①，在△ABC中，分别以AB、AC为斜边，向△ABC的形外作等腰直角三角形，直角的顶点分别为D、E，点F、M、G分别为AB、BC、AC边的中点．求证：△DFM≌△MGE．
【拓展探究】如图②，在△ABC中，分别以AB、AC为底边，向△ABC的形外作等腰三角形，顶角的顶点分别为D、E，且∠BAD+∠CAE=90°．点F、M、G分别为AB、BC、AC边的中点，若AD=5，AB=6，△DFM的面积为32，直接写出△MGE的面积．

7．一次函数y=2x+3的图象不经过的象限是（　　）

14．

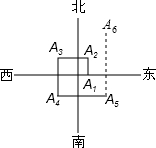如图，一个机器人从点O出发，向正东方向走3m到达点A₁，再向正北方向走6m到达点A₂，再向正西方向走9m到达点A₃，再向正南方向走12m到达点A₄，再向正东方向走15m到达点A₅．按如此规律下去，当机器人走到点A₆时，离点O的距离是15m．

4．

微山县鹿鸣小区内有一块长为（3a+b）米，宽为（2a+b）米的长方形空地，物业部门计划将这块空地进行绿化（如图阴影部分），中间部分将修建一仿古小景点（如图中间的长方形），则绿化的面积是多少平方米？并求出当a=8，b=7时的绿化面积．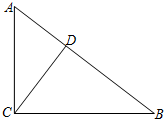

11．

（1）计算：4sin60°+tan45°-$\sqrt{12}$
（2）如图，在Rt△ABC中，∠ACB=90°，AB=10，cosB=$\frac{4}{5}$，CD⊥AB于点D，求CD的长．

8．甲、乙两人玩猜数字游戏，游戏规则如下：有四个数字1、2、4、5，先由甲心中任选一个数字，记为m，再由乙猜甲刚才所选的数字，记为n．若m、n满足|m-n|≤2，则称甲、乙两人“心有灵犀”．则甲、乙两人“心有灵犀”的概率是$\frac{1}{2}$．

9．已知直线y=2x-4+n经过原点，与反比例函数y=$\frac{n}{x}$的图象交于点A、B．求：
（1）反比例函数解析式；
（2）线段AB的长．

试题分类