题目内容
8.甲、乙两人玩猜数字游戏,游戏规则如下:有四个数字1、2、4、5,先由甲心中任选一个数字,记为m,再由乙猜甲刚才所选的数字,记为n.若m、n满足|m-n|≤2,则称甲、乙两人“心有灵犀”.则甲、乙两人“心有灵犀”的概率是$\frac{1}{2}$.分析 首先根据题意画出树状图,然后由树状图求得所有等可能的结果与m、n满足|m-n|≤2情况,再利用概率公式即可求得答案.
解答 解:画树状图得:
∵共有16种等可能的结果,m、n满足|m-n|≤2的有8种情况,
∴甲、乙两人“心有灵犀”的概率为$\frac{8}{16}=\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题考查的是用列表法或画树状图法求概率.注意列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.注意概率=所求情况数与总情况数之比.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
16. 用长6m的铝合金条制成“日”字型矩形窗户,使窗户的透光面积最大(如图),那么这个窗户的最大透光面积是( )
用长6m的铝合金条制成“日”字型矩形窗户,使窗户的透光面积最大(如图),那么这个窗户的最大透光面积是( )
 用长6m的铝合金条制成“日”字型矩形窗户,使窗户的透光面积最大(如图),那么这个窗户的最大透光面积是( )
用长6m的铝合金条制成“日”字型矩形窗户,使窗户的透光面积最大(如图),那么这个窗户的最大透光面积是( )| A. | $\frac{2}{3}$m2 | B. | 1m2 | C. | $\frac{3}{2}$m2 | D. | 3m2 |
3.从1,2,3,4,5,6中任意取一个数,取到的数小于3的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{6}$ |
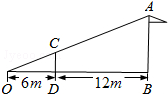 如图,小明用长为3m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的距离DB=12m,则旗杆AB的高为( )
如图,小明用长为3m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的距离DB=12m,则旗杆AB的高为( ) 如图是一个可以自由转动的正六边形转盘,其中三个正三角形涂有阴影.转动指针,指针落在有阴影的区域内的概率为$\frac{1}{2}$.
如图是一个可以自由转动的正六边形转盘,其中三个正三角形涂有阴影.转动指针,指针落在有阴影的区域内的概率为$\frac{1}{2}$.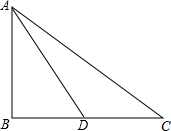 如果一个三角形一边上的中线长恰好等于这边的长,那么这个三角形称为“有趣三角形”,这条中线称为“有趣中线”.如图,已知Rt△ABC中,∠B=90°,若Rt△ABC是“有趣三角形”,AD为“有趣中线”,且AD=14cm,则AC=9$\sqrt{3}$cm.
如果一个三角形一边上的中线长恰好等于这边的长,那么这个三角形称为“有趣三角形”,这条中线称为“有趣中线”.如图,已知Rt△ABC中,∠B=90°,若Rt△ABC是“有趣三角形”,AD为“有趣中线”,且AD=14cm,则AC=9$\sqrt{3}$cm.