题目内容
10.【发现问题】如图①,在△ABC中,分别以AB、AC为斜边,向△ABC的形外作等腰直角三角形,直角的顶点分别为D、E,点F、M、G分别为AB、BC、AC边的中点.求证:△DFM≌△MGE.【拓展探究】如图②,在△ABC中,分别以AB、AC为底边,向△ABC的形外作等腰三角形,顶角的顶点分别为D、E,且∠BAD+∠CAE=90°.点F、M、G分别为AB、BC、AC边的中点,若AD=5,AB=6,△DFM的面积为32,直接写出△MGE的面积.
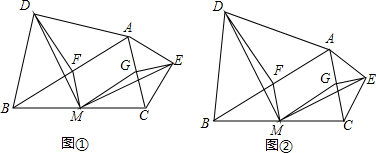
分析 【发现问题】根据等腰直角三角形的性质得到∠DFB=90°,DF=FA;∠EGC=90°,AG=GE,根据三角形的中位线的性质得到FM∥AC,MG∥AB,推出四边形AFMG是平行四边形,根据平行四边形的性质得到FM=AG,MG=FA,∠BFM=∠BAC,∠BAC=∠MGC,即可得到结论;
【拓展探究】根据三角形的中位线的性质得到FM∥AC,MG∥AB,FM=$\frac{1}{2}$AC=AG,MG=$\frac{1}{2}$AB=AF,∠MGC=∠BAC=∠BFM,等量代换得到∠DFM=∠MGE,根据余角的性质得到∠1=∠3,根据三角函数的定义$\frac{DF}{AF}=\frac{AG}{GE}$,推出$\frac{DF}{MG}=\frac{FM}{EG}$,得到△DFM∽△MGE,根据相似三角形的性质即可得到结论.
解答 【发现问题】证明:∵△ADB是等腰直角三角形,F为斜边AB的中点,
∴∠DFB=90°,DF=FA;
∵△ACE是等腰直角三角形,G为斜边AC的中点,
∴∠EGC=90°,AG=GE,
∵点F、M、G分别为AB、BC、AC边的中点,
∴FM∥AC,MG∥AB,
∴四边形AFMG是平行四边形,
∴FM=AG,MG=FA,∠BFM=∠BAC,∠BAC=∠MGC,
∴DF=MG,∠DFM=∠MGE,FM=GE,
在△DFM与△MGE中,
$\left\{\begin{array}{l}{DF=MG}\\{∠DFM=∠MGE}\\{FM=GE}\end{array}\right.$,
∴△DFM≌△MGE.
【拓展探究】 ∵点F、M、G分别为AB、BC、AC边的中点,
∵点F、M、G分别为AB、BC、AC边的中点,
∴FM∥AC,MG∥AB,FM=$\frac{1}{2}$AC=AG,MG=$\frac{1}{2}$AB=AF,∠MGC=∠BAC=∠BFM,
∴∠DFM=∠MGE,
∵∠1+∠2=90°∠2+∠3=90°,
∴∠1=∠3,
∴tan∠1=tan∠3,
即$\frac{DF}{AF}=\frac{AG}{GE}$,
∴$\frac{DF}{MG}=\frac{FM}{EG}$,
∵∠DFM=∠MGE,
∴△DFM∽△MGE,
∴$\frac{{S}_{△MGE}}{{S}_{△DMF}}$=($\frac{MG}{DF}$)2=$\frac{9}{16}$,
∴S△MGE=18.
点评 本题考查了全等三角形的判定和性质,相似三角形的判定和性质,直角三角形的性质.三角形的中位线的性质,等腰三角形的性质,证得△DFM∽△MGE是解题的关键.

 如图,已知点A(8,0),O为坐标原点,P是线段OA上任意一点(不含端点O、A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=5时,这两个二次函数的最大值之和等于3.
如图,已知点A(8,0),O为坐标原点,P是线段OA上任意一点(不含端点O、A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=5时,这两个二次函数的最大值之和等于3.
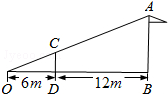 如图,小明用长为3m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的距离DB=12m,则旗杆AB的高为( )
如图,小明用长为3m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的距离DB=12m,则旗杆AB的高为( )