题目内容
4.某工厂现有机器20台,每台机器平均日产量为60件产品,现工厂计划增购若干台同样的机器以提高总产量.据调研分析,由于场地限制等因素,每增加一台机器,每台机器的平均日产量要比原来少2件.问:当增加多少台机器时,可使每天生产的产品总量最大?最大总产量是多少?分析 根据题意增加x台机器,每台每天将少生产2x件产品,生产量为(60-2x)件,此时机器数为(20+x)台,每天生产总量可求出;根据题意即可得到函数解析式,然后根据函数性质和顶点坐标公式求最值即可.
解答 解:设增加x台机器时,每天生产的产品总量为y,
根据题意得:y=(20+x)(60-2x)=-2x2+20x+1200,
即y=-2(x-5)2+1250,
因为-2<0,
所以当x=5时,y最大=1250.
答:增加5台机器时,可使每天生产的产品总量最大,最大总产量是1250件.
点评 本题考查了二次函数的性质在实际生活中的应用,熟练掌握二次函数的图象和性质是解答的关键.

练习册系列答案
相关题目
14.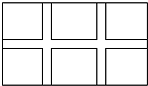 如图,学校课外生物小组的实验圆地是长35米、宽20米的矩形,为便于管理,现要在中间开辟一横两纵三条等宽的小道.要使种植面积为600平方米,若设小道的宽为x米,则所列方程正确的是( )
如图,学校课外生物小组的实验圆地是长35米、宽20米的矩形,为便于管理,现要在中间开辟一横两纵三条等宽的小道.要使种植面积为600平方米,若设小道的宽为x米,则所列方程正确的是( )
 如图,学校课外生物小组的实验圆地是长35米、宽20米的矩形,为便于管理,现要在中间开辟一横两纵三条等宽的小道.要使种植面积为600平方米,若设小道的宽为x米,则所列方程正确的是( )
如图,学校课外生物小组的实验圆地是长35米、宽20米的矩形,为便于管理,现要在中间开辟一横两纵三条等宽的小道.要使种植面积为600平方米,若设小道的宽为x米,则所列方程正确的是( )| A. | 35×20-2×20x-35x=600 | B. | 35×20-20x-35x+x2=600 | ||
| C. | (35-2x)(20-x)=600 | D. | (35-x)(20-x)=600 |
 如图所示的几何体是由四个小正方体组合而成的,请画出这个几何体从正面、左面和上面看到的图形.
如图所示的几何体是由四个小正方体组合而成的,请画出这个几何体从正面、左面和上面看到的图形.