题目内容
7.如图.在平而直角坐标系中,已知A(0,2),B($\frac{b-1}{2}$,0)将点B向上平移4个单位得到点C,其中b与4的差的2倍等于6(1)请直接写出B,C两点坐标;
(2)如果在第二象限内有一点P(t,$\frac{2}{3}$),求四边形ABOP的面积(用含t的式子表示)
(3)在(2)的条件下,若存在点P,使四边形ABOP的面积是△ABC面积的$\frac{3}{4}$,求点的P的坐标.
分析 (1)先确定出点B的坐标,再由平移得到点C的坐标,即可;
(2)先确定出OA,OB,再用面积之和得出四边形ABOP的面积与t的关系式;
(3)先确定出三角形ABC的面积,借助(2)的结论列出方程求解即可.
解答 解:(1)∵b与4的差的2倍等于6,
∴2(b-4)=6,
∴b=7,
∴B(3,0),
∵点B向上平移4个单位得到点C,
∴C(3,4),
(2)如图,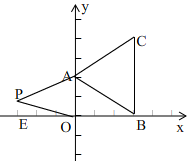
∵A(0,2),B(3,0),
∴OA=2,OB=3
∴S四边形ABOP=S△AOB-S△AOP=$\frac{1}{2}$OA×OB+$\frac{1}{2}$OA×|xP|=$\frac{1}{2}$×2×3+$\frac{1}{2}$×2(-t)=-t+3,(t<0)
(3)存在,
理由:
由(1)知,B(3,0),C(3,4),
∴BC=4,
∵A(0,2),
∴S△ABC=$\frac{1}{2}$×BC×|xB-xA|=$\frac{1}{2}$×4×3=6,
∵四边形ABOP的面积是△ABC面积的$\frac{3}{4}$,
∴-t+3=$\frac{3}{4}$×6,
∴t=-$\frac{3}{2}$
点评 此题是几何变换综合题,主要考查了平移的性质,四边形的面积的计算方法,三角形的面积计算方法,求出四边形ABOP与t的关系式是解本题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
17.下列说法中,正确的是( )
| A. | $\sqrt{16}$=±4 | B. | -22的平方根是±2 | ||
| C. | 64的立方根是±4 | D. | -$\sqrt{5}$是5的一个平方根 |
18.若(a2+1)2-2(a2+1)-3=0,则a2等于( )
| A. | 2 | B. | -2 | C. | ±2 | D. | 以上都不对 |
12.已知:角α的终边经过点($\frac{1}{2}$,-$\frac{\sqrt{2}}{2}$),则tanα=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{\sqrt{6}}{3}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | -$\sqrt{2}$ |
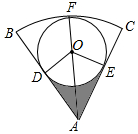 如图,AB,AC是扇形的两条半径,⊙O分别与AB,AC相切于点D,E,与$\widehat{BC}$相切于点F,若⊙O的面积是4π,∠A=60°,求图形阴影部分的面积.
如图,AB,AC是扇形的两条半径,⊙O分别与AB,AC相切于点D,E,与$\widehat{BC}$相切于点F,若⊙O的面积是4π,∠A=60°,求图形阴影部分的面积. 如图,数轴上有A、B两个动点,对应的数分别为-9和5,A点的运动速度为每秒1个单位,B点的运动速度为每秒3个单位.
如图,数轴上有A、B两个动点,对应的数分别为-9和5,A点的运动速度为每秒1个单位,B点的运动速度为每秒3个单位.