题目内容
1．
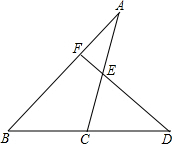如图，已知D是△ABC边BC延长线上一点，DF⊥AB于点F，交AC于点E，∠A=35°，∠D=42°，求（1）∠ACD的度数； （2）∠AEF的度数．
分析 （1）根据直角三角形的性质可得∠B=90°-∠D=48°，再根据三角形外角的性质可得∠ACD=∠A+∠B=83°；
（2）根据直角三角形的性质可得∠AEF=90°-∠A，进而可得答案．
解答 解：（1）∵DF⊥AB，
∴∠B=90°-∠D=48°，
∵∠ACD是△ABC的一个外角，
∴∠ACD=∠A+∠B=83°；
（2）∵DF⊥AB，
∴∠AFD=90°，
∴∠AEF=90°-∠A=55°．
点评 此题主要考查了三角形外角的性质，关键是掌握三角形的一个外角等于和它不相邻的两个内角的和．
练习册系列答案
相关题目
9．下面四个图形中是轴对称图形的个数有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
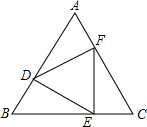如图，在等边△ABC的三边上分别取点D、E、F，使AD=BE=CF．
如图所示，有一抛物线形门洞，地面宽度为8m，有一宽6m，高4m的车刚好能通过这个门洞，求这个门洞的高度．（精确到0.01m）
如图，小明要在一幅长90厘米、宽40厘米的风景画的四周外围镶上一个宽度相同的边框，制成一挂图，使风景画的面积为整个挂图面积的54%．设边框的宽度为x厘米，根据题意所列方程是（90+2x）（40+2x）×54%=90×40．
10．
如图，已知点A（8，0），O为坐标原点，P是线段OA上任意一点（不含端点O，A），过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下，它们的顶点分别为B、C，射线OB与AC相交于点D．当OD=AD=6时，这两个二次函数的最大值之和等于（ ）
如图，已知点A（8，0），O为坐标原点，P是线段OA上任意一点（不含端点O，A），过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下，它们的顶点分别为B、C，射线OB与AC相交于点D．当OD=AD=6时，这两个二次函数的最大值之和等于（ ）| A． | 5 | B． | $\frac{{8\sqrt{5}}}{3}$ | C． | 10 | D． | $2\sqrt{5}$ |