题目内容
7. 如图,矩形ABCD中,AB=8,BC=4,点E在边AB上,点F在边CD上,点G、H在对角线AC上,若四边形EGFH是菱形,则AE的长是5.
如图,矩形ABCD中,AB=8,BC=4,点E在边AB上,点F在边CD上,点G、H在对角线AC上,若四边形EGFH是菱形,则AE的长是5.
分析 首先连接EF交AC于O,由矩形ABCD中,四边形EGFH是菱形,易证得△CFO≌△AOE(AAS),即可得OA=OC,然后由勾股定理求得AC的长,继而求得OA的长,又由△AOE∽△ABC,利用相似三角形的对应边成比例,即可求得答案.
解答  解:连接EF交AC于O,
解:连接EF交AC于O,
∵四边形EGFH是菱形,
∴EF⊥AC,OE=OF,
∵四边形ABCD是矩形,
∴∠B=∠D=90°,AB∥CD,
∴∠ACD=∠CAB,
在△CFO与△AOE中,
$\left\{\begin{array}{l}{∠FCO=∠OAB}\\{∠FOC=∠AOE}\\{OF=OE}\end{array}\right.$,
∴△CFO≌△AOE(AAS),
∴AO=CO,
∵AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=4$\sqrt{5}$,
∴AO=$\frac{1}{2}$AC=2$\sqrt{5}$,
∵∠CAB=∠CAB,∠AOE=∠B=90°,
∴△AOE∽△ABC,
∴$\frac{AO}{AB}=\frac{AE}{AC}$,
∴$\frac{2\sqrt{5}}{8}=\frac{AE}{4\sqrt{5}}$,
∴AE=5.
故答案为5.
点评 此题考查了菱形的性质、矩形的性质、全等三角形的判定与性质以及相似三角形的判定与性质.注意准确作出辅助线是解此题的关键.

练习册系列答案
相关题目
18.(-$\frac{1}{2}$)3的倒数是( )
| A. | -8 | B. | -$\frac{1}{8}$ | C. | 8 | D. | $\frac{1}{8}$ |
2. 直线a、b、c、d的位置如图,如果∠1=100°,∠2=100°,∠3=125°,那么∠4等于( )
直线a、b、c、d的位置如图,如果∠1=100°,∠2=100°,∠3=125°,那么∠4等于( )
 直线a、b、c、d的位置如图,如果∠1=100°,∠2=100°,∠3=125°,那么∠4等于( )
直线a、b、c、d的位置如图,如果∠1=100°,∠2=100°,∠3=125°,那么∠4等于( )| A. | 80° | B. | 65° | C. | 60° | D. | 55° |
12.给出四个数0,$\sqrt{2}$,$\frac{1}{3}$,-1,其中最小的数是( )
| A. | 0 | B. | $\sqrt{2}$ | C. | $\frac{1}{3}$ | D. | -1 |
16.按如图所示的方法折纸,下面结论正确的个数( )
①∠2=90°;②∠1=∠AEC;③△ABE∽△ECF;④∠BAE=∠3.

①∠2=90°;②∠1=∠AEC;③△ABE∽△ECF;④∠BAE=∠3.

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
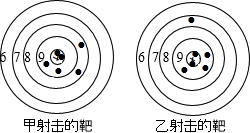 如图是甲乙两人在一次射击比赛中靶的情况(击中靶中心的圆面为10环,靶中数字表示该数所在圆环被击中所得的环数),每人射击了6次.
如图是甲乙两人在一次射击比赛中靶的情况(击中靶中心的圆面为10环,靶中数字表示该数所在圆环被击中所得的环数),每人射击了6次. 如图,将三角形ABC纸片沿MN折叠,使点A落在点A′处,若∠A′MB=55°,则∠AMN=62.5°.
如图,将三角形ABC纸片沿MN折叠,使点A落在点A′处,若∠A′MB=55°,则∠AMN=62.5°.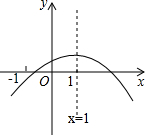 已知二次函数y=ax2+bx+c(a≠0)的图象如图,以下结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图,以下结论: