题目内容
20. 如图,圆柱形水管内原有积水的水平面宽CD=20cm,水深EB=2cm.求圆形的半径是多少.
如图,圆柱形水管内原有积水的水平面宽CD=20cm,水深EB=2cm.求圆形的半径是多少.
分析 连接OC,如图,设⊙O的半径为R,由于B点为弧CD的中点,AB⊥CD,根据垂径定理的推理和垂径定理得到AB必过圆心0,即点O、E、B共线,CE=ED=$\frac{1}{2}$CD=810,在Rt△OCE中,利用勾股定理得(R-2)2+102=R2,然后解方程即可.
解答  解:连接OC,如图,设⊙O的半径为R,
解:连接OC,如图,设⊙O的半径为R,
∵BE为水深,即B点为弧CD的中点,AB⊥CD,
∴AB必过圆心0,即点O、E、B共线,CE=ED=$\frac{1}{2}$CD=10cm,
在Rt△OCE中,OC=R,OE=R-BE=R-2,CE=10,
∵OE2+CE2=OC2,
∴(R-2)2+102=R2,解得R=26cm,
即水管截面所在圆的半径为26cm.
点评 本题考查了垂径定理的应用:从实际问题中抽象出几何图形,然后垂径定理和勾股定理相结合,构造直角三角形,可解决计算弦长、半径、弦心距等问题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
10.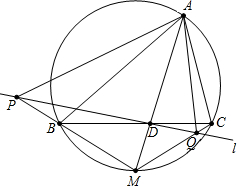 如图,已知∠A的平分线分别与边BC、△ABC的外接圆交于点D、M,过D任作一条与直线BC不重合的直线l,直线l分别与直线MB、MC交于点P、Q,下列判断错误的是( )
如图,已知∠A的平分线分别与边BC、△ABC的外接圆交于点D、M,过D任作一条与直线BC不重合的直线l,直线l分别与直线MB、MC交于点P、Q,下列判断错误的是( )
 如图,已知∠A的平分线分别与边BC、△ABC的外接圆交于点D、M,过D任作一条与直线BC不重合的直线l,直线l分别与直线MB、MC交于点P、Q,下列判断错误的是( )
如图,已知∠A的平分线分别与边BC、△ABC的外接圆交于点D、M,过D任作一条与直线BC不重合的直线l,直线l分别与直线MB、MC交于点P、Q,下列判断错误的是( )| A. | 无论直线l的位置如何,总有直线PM与△ABD的外接圆相切 | |
| B. | 无论直线l的位置如何,总有∠PAQ>∠BAC | |
| C. | 直线l选取适当的位置,可使A、P、M、Q四点共圆 | |
| D. | 直线l选取适当的位置,可使S△APQ<S△ABC |
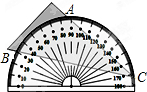 如图,三角形纸板放置在量角器上,三角形的顶点点C恰在半圆上,两边与半圆的交点记为A、B,A点的读数为80°,B点的读数为30°,则∠ACB的大小为25°.
如图,三角形纸板放置在量角器上,三角形的顶点点C恰在半圆上,两边与半圆的交点记为A、B,A点的读数为80°,B点的读数为30°,则∠ACB的大小为25°.
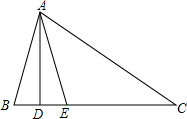 如图,△ABC中,AD⊥BC,点E在AC的垂直平分线上,且BD=DE.
如图,△ABC中,AD⊥BC,点E在AC的垂直平分线上,且BD=DE.