题目内容
12.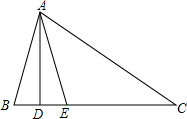 如图,△ABC中,AD⊥BC,点E在AC的垂直平分线上,且BD=DE.
如图,△ABC中,AD⊥BC,点E在AC的垂直平分线上,且BD=DE.(1)如果∠BAE=40°,那么∠B=70°,∠C=35°;
(2)如果△ABC的周长为13cm,AC=6cm,那么△ABE的周长=7cm;
(3)你发现线段AB与BD的和等于图中哪条线段的长,并证明你的结论.
分析 (1)根据垂直平分线的性质得出AB=AE,从而得出角之间的关系∠ABE=∠AEB=2∠C,代数求解即可;
(2)通过线段的等量代换即可求解;
(3)由AD⊥BC,BD=DE,点E在AC的垂直平分线上,根据线段垂直平分线的性质,可得AE=EC,AB=AE,继而证得AB+BD=AE+DE=DC.
解答 (1)解:∵点E在AC的垂直平分线上,
∴AE=EC.
∵BD=DE,AD⊥BC,
∴AB=AE.
∴∠ABE=∠AEB=2∠C=(180°-40°)÷2=140°÷2=70°,∠C=35°.
故答案为:70,35;
(2)解:∵△ABC的周长为13cm,AC=6cm,
∴AB+BC=13-6=7,
∴△ABE的周长=AB+BC=7cm.
故答案为:7;
(3)AB+BD=DC.
证明:∵AD⊥BC,BD=DE,
∴AB=AE,BD=DE,
∵点E在AC的垂直平分线上,
∴AE=CE,
∴AB+BD=AE+DE=DC.
点评 此题考查了线段垂直平分线的性质、含30°角的直角三角形的性质以及等腰三角形的判定与性质.此题难度适中,注意掌握转化思想与数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4. 如图,△ABC≌△CDA,下列结论错误的是( )
如图,△ABC≌△CDA,下列结论错误的是( )
 如图,△ABC≌△CDA,下列结论错误的是( )
如图,△ABC≌△CDA,下列结论错误的是( )| A. | ∠DAC=∠BCA | B. | ∠ADC=∠ACB | C. | ∠B=∠D | D. | AD=BC |
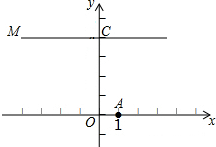 如图,在平面直角坐标系内,O为原点,点A的坐标为(1,0),点C的坐标为(0,4),直线CM⊥x轴,直线y=-x+b(b为常数)经过点A,且与直线CM相交于点D,连结OD.
如图,在平面直角坐标系内,O为原点,点A的坐标为(1,0),点C的坐标为(0,4),直线CM⊥x轴,直线y=-x+b(b为常数)经过点A,且与直线CM相交于点D,连结OD. 如图,∠ABC=∠DCB,再添加条件∠A=∠D或∠ACB=∠DCB 或条件AB=DC,就可以判定△ABC≌△DCB.
如图,∠ABC=∠DCB,再添加条件∠A=∠D或∠ACB=∠DCB 或条件AB=DC,就可以判定△ABC≌△DCB. 如图,圆柱形水管内原有积水的水平面宽CD=20cm,水深EB=2cm.求圆形的半径是多少.
如图,圆柱形水管内原有积水的水平面宽CD=20cm,水深EB=2cm.求圆形的半径是多少. 如图,直线AB、CD相交于点O,OE平分∠BOC,OF⊥CD,若∠BOE=2∠BOD,求∠AOF的度数.
如图,直线AB、CD相交于点O,OE平分∠BOC,OF⊥CD,若∠BOE=2∠BOD,求∠AOF的度数. 如图为二次函数y=ax+bx+c的图象,给出下列说法:
如图为二次函数y=ax+bx+c的图象,给出下列说法: