题目内容
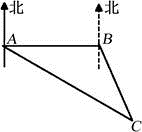
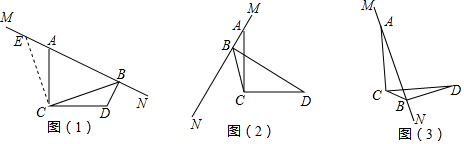
8.【问题情境】如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.求证:AM=AD+MC.
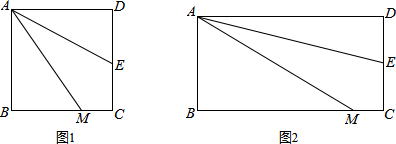
【探究展示】
(2)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,试判断AM=AD+MC是否成立?若成立,请给出证明,若不成立,请说明理由;
【拓展延伸】
(3)若(2)中矩形ABCD两边AB=6,BC=9,求AM的长.
分析 (1)先构造出△ADE≌△NCE,即可得出结论;
(2)同(1)的方法即可得出结论;
(3)设出MC=x,利用(2)的结论得出AM=9+x,再利用勾股定理建立方程求出CM即可得出结论.
解答 解:(1)如图1,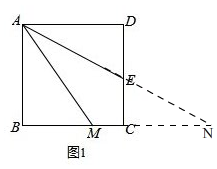 延长AE,BC相交于N,
延长AE,BC相交于N,
∵四边形ABCD是正方形,
∴AD∥BC,
∴∠DAE=∠ENC,
∵AE平分∠DAE,
∴∠∠DAE=∠MAE,
∴∠ENC=∠MAE,在△ADE和△NCE中,$\left\{\begin{array}{l}{∠DAE=∠CNE}\\{∠AED=∠NEC}\\{DE=CE}\end{array}\right.$,
∴△ADE≌△NCE,
∴AD=CN,
∴AM=MN=NC+MC=AD+MC;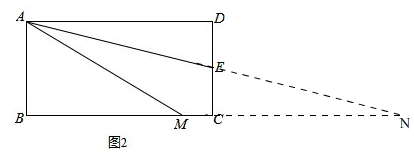
(2)结论AM=AD+CM仍然成立,
理由:如图2,
延长AE,BC相交于N,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DAE=∠ENC,
∵AE平分∠DAE,
∴∠DAE=∠MAE,
∴∠ENC=∠MAE,
在△ADE和△NCE中,$\left\{\begin{array}{l}{∠DAE=∠CNE}\\{∠AED=∠NEC}\\{DE=CE}\end{array}\right.$,
∴△ADE≌△NCE,
∴AD=CN,
∴AM=MN=NC+MC=AD+MC;
(3)设MC=x,则BM=BC-CN=9-x,
由(2)知,AM=AD+MC=9+x,
在Rt△ABC中,AM2-BM2=AB2,
(9+x)2-(9-x)2=36,
∴x=1,
∴AM=AD+MC=10.
点评 此题是四边形综合题,主要考查了正方形的性质,矩形的性质,全等三角形的判定和性质,勾股定理,解本题的关键是判断出△ADE≌△NCE和利用勾股定理建立方程,是一道基础题目.

练习册系列答案
相关题目
17.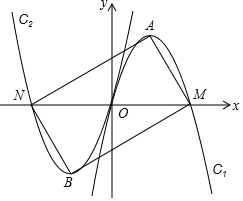 如图,经过坐标原点的抛物线C1:y=ax2+bx与x轴的另一交点为M,它的顶点为点A,将C1绕原点旋转180°,得到抛物线C2,C2与x轴的另一交点为N,顶点为点B,连接AM,MB,BN,NA,当四边形AMBN恰好是矩形时,则b的值( )
如图,经过坐标原点的抛物线C1:y=ax2+bx与x轴的另一交点为M,它的顶点为点A,将C1绕原点旋转180°,得到抛物线C2,C2与x轴的另一交点为N,顶点为点B,连接AM,MB,BN,NA,当四边形AMBN恰好是矩形时,则b的值( )
 如图,经过坐标原点的抛物线C1:y=ax2+bx与x轴的另一交点为M,它的顶点为点A,将C1绕原点旋转180°,得到抛物线C2,C2与x轴的另一交点为N,顶点为点B,连接AM,MB,BN,NA,当四边形AMBN恰好是矩形时,则b的值( )
如图,经过坐标原点的抛物线C1:y=ax2+bx与x轴的另一交点为M,它的顶点为点A,将C1绕原点旋转180°,得到抛物线C2,C2与x轴的另一交点为N,顶点为点B,连接AM,MB,BN,NA,当四边形AMBN恰好是矩形时,则b的值( )| A. | 2$\sqrt{2}$ | B. | -2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | -2$\sqrt{3}$ |
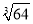 ,
, 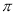 ,
, 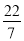 ,1.010010001…(从左向右每两个1之间依次增加一个0)中,无理数的个数有( )
,1.010010001…(从左向右每两个1之间依次增加一个0)中,无理数的个数有( )
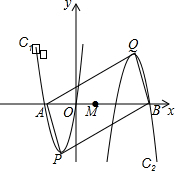 如图,抛物线C1:y1=ax2+2ax(a>0)与x轴交于点A,顶点为点P.
如图,抛物线C1:y1=ax2+2ax(a>0)与x轴交于点A,顶点为点P.