题目内容
16.如图1,在平面直角坐标系中,点A、B的坐标分别为(-4,0)和(-1,0),过点A作CA⊥AB,连结BC,tan∠ABC=$\frac{4}{3}$,将△ABC沿x轴正方向平移至顶点C1恰好落在双曲线y=$\frac{k}{x}$上,同时B1C1交双曲线y=$\frac{k}{x}$于另一点D(3,$\frac{8}{3}$).(1)求△ABC平移的距离;
(2)如图2,将△A1B1C1继续向右平移后得△A2B2C2,连结B2D,C2D,问当点B2在何位置时,△B2C2D的面积是△ABC面积的2倍?请求出点B2的坐标.
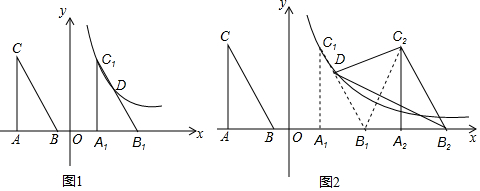
分析 (1)由AB的坐标可求出AB的长度,由CA⊥AB、tan∠ABC=$\frac{4}{3}$,可求出AC的长度,再根据反比例函数图象上点的坐标特征可求出k值,将y=4代入双曲线解析式中可求出点C1的坐标,结合点C的坐标,即可得出△ABC平移的距离;
(2)连接B1C2,根据平行线的性质可得出${S}_{△{B}_{2}{C}_{2}D}$=${S}_{△{B}_{2}{C}_{2}{B}_{1}}$=2S△ABC,进而可得出点B1、B2的坐标,此题得解.
解答 解:(1)∵A(-4,0)、B(-1,0),
∴AB=-1-(-4)=3.
∵CA⊥AB,tan∠ABC=$\frac{4}{3}$,
∴AC=$\frac{4}{3}$AB=4,
∴点C的坐标为(-4,4).
∵点D(3,$\frac{8}{3}$)在双曲线y=$\frac{k}{x}$上,
∴k=3×$\frac{8}{3}$=8,
∴双曲线的解析式为y=$\frac{8}{x}$.
当y=$\frac{8}{x}$=4时,x=2,
∴点C1的坐标为(2,4),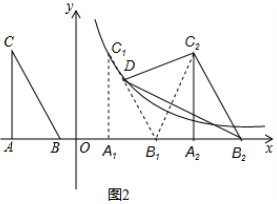
∴△ABC平移的距离为2-(-4)=6.
(2)连接B1C2,如图2所示.
∵△A1B1C1继续向右平移后得△A2B2C2,
∴B1C1∥B2C2,
∴${S}_{△{B}_{2}{C}_{2}D}$=${S}_{△{B}_{2}{C}_{2}{B}_{1}}$=2S△ABC,
∴$\frac{{B}_{1}{B}_{2}•{A}_{2}{C}_{2}}{2}$=2×$\frac{AB•AC}{2}$,
∴B1B2=2AB=6.
∵B(-1,0)且CC1=BB1=6,
∴B1的坐标为(5,0),
∴B2的坐标为(11,0).
点评 本题考查了反比例函数图象上点的坐标特征、坐标与图形变化中的平移、平行线的性质以及解直角三角形,解题的关键是:(1)通过解直角三角形以及反比例函数图象上点的坐标特征求出点C、C1的坐标;(2)根据平行线的性质找出${S}_{△{B}_{2}{C}_{2}D}$=${S}_{△{B}_{2}{C}_{2}{B}_{1}}$=2S△ABC.

 B.
B.  C.
C.  D.
D. 

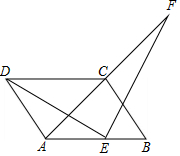 如图,四边形ABCD是平行四边形,AD=AC,AD⊥AC,E是AB的中点,F是AC延长线上一点.
如图,四边形ABCD是平行四边形,AD=AC,AD⊥AC,E是AB的中点,F是AC延长线上一点.