题目内容
14.已知,四边形ABCD是菱形,点M、N分别在AB、AD上,且BM=DN,MG∥AD,NF∥AB,点F、G分别在BC、CD上,MG与NF相交于点E.(1)如图1,求证:四边形AMEN是菱形;
(2)如图2,连接AC在不添加任何辅助线的情况下,请直接写出面积相等的四边形.
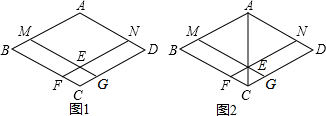
分析 (1)由MG∥AD,NF∥AB,可证得四边形AMEN是平行四边形,又由四边形ABCD是菱形,BM=DN,可得AM=AN,即可证得四边形AMEN是菱形;
(2)易得四边形CGEF是菱形;即可得S△AEM=S△AEN,S△CEF=S△CEG,S△ABC=S△ADC,继而求得答案.
解答 (1)证明:∵MG∥AD,NF∥AB,
∴四边形AMEN是平行四边形,
∵四边形ABCD是菱形,
∴AB=AD,
∵BM=DN,
∴AB-BM=AD-DN,
∴AM=AN,
∴四边形AMEN是菱形;
(2)解:∵四边形AMEN是菱形,
∴S△AEM=S△AEN,
同理:四边形CGEF是菱形,
∴S△CEF=S△CEG,
∵四边形ABCD是菱形,
∴S△ABC=S△ADC,
∴S四边形MBFE=S四边形DNEG,S四边形MBCE=S四边形DNEC,S四边形MBCG=S四边形DNFC,S四边形ABFE=S四边形ADGE,S四边形ABFN=S四边形ADGM.
点评 此题考查了菱形的性质与判定.注意证得四边形AMEN是菱形与四边形CGEF是菱形是关键.

练习册系列答案
相关题目
5.古希腊数学家把数1,3,6,10,15,21,…叫做三角数,它有一定的规律性.若把第一个三角数记为a1,第二个三角数记为a2…,第n个三角数记为an,则an+an+1=( )
| A. | n2+n | B. | n2+n+1 | C. | n2+2n | D. | n2+2n+1 |

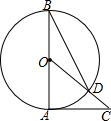 如图,AB是⊙O的直径,AC是⊙O的切线,连接OC与⊙O相交于点D,连接BD,∠C=40°,若点P为优弧$\widehat{ABD}$上的动点,连接PA、PD,则∠APD的大小是25度.
如图,AB是⊙O的直径,AC是⊙O的切线,连接OC与⊙O相交于点D,连接BD,∠C=40°,若点P为优弧$\widehat{ABD}$上的动点,连接PA、PD,则∠APD的大小是25度.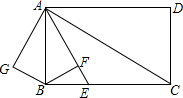 如图在矩形ABCD中,AB=6,AD=8,AE平分∠BAC交BC于点E,过B作BF⊥AE交AE于点F,将△ABF沿AB翻折得到△ABG,将△ABG绕点A逆时针旋转角a,(其中0°<a<180°)记旋转中的△ABG为△AB′G′,在旋转过程中,设直线B′G′分别与直线AD、直线AC交于点M、N,当MA=MN时,线段MD长为8-$\frac{5\sqrt{5}}{2}$.
如图在矩形ABCD中,AB=6,AD=8,AE平分∠BAC交BC于点E,过B作BF⊥AE交AE于点F,将△ABF沿AB翻折得到△ABG,将△ABG绕点A逆时针旋转角a,(其中0°<a<180°)记旋转中的△ABG为△AB′G′,在旋转过程中,设直线B′G′分别与直线AD、直线AC交于点M、N,当MA=MN时,线段MD长为8-$\frac{5\sqrt{5}}{2}$.