题目内容
8.关于x的方程mx2+(m-1)x+m=0有实根,则实数m的取值范围是( )| A. | {m|-1<m<$\frac{1}{3}$} | B. | {m|-1≤m≤$\frac{1}{3}$} | C. | {m|-1≤m≤$\frac{1}{3}$且m≠0} | D. | {m|m≤-1或m≥$\frac{1}{3}$} |
分析 由于m的值不能确定,所以分m=0与m≠0两种情况进行讨论即可.
解答 解:当m=0时,原方程可化为-x=0,解得x=0;
当m≠0时,△≥0,即△=(m-1)2-4m2≥0,解得-1≤m≤$\frac{1}{3}$.
故选B.
点评 本题考查的是根的判别式,熟知一元二次方程的解与判别式的关系是解答此题的关键.

练习册系列答案
相关题目
16.若不等式组$\left\{\begin{array}{l}{x≥3}\\{x<m}\end{array}\right.$无解,则m的取值范围是( )
| A. | m≥3 | B. | m≤3 | C. | m>3 | D. | m<3 |
18.下列比较有理数-0.1,-$\frac{1}{3}$,-$\frac{1}{4}$大小正确的是( )
| A. | -$\frac{1}{3}$<-$\frac{1}{4}$<-0.1 | B. | -$\frac{1}{4}$<-$\frac{1}{3}$<-0.1 | C. | -0.1<-$\frac{1}{4}$<-$\frac{1}{3}$ | D. | -0.1<-$\frac{1}{3}$<-$\frac{1}{4}$ |
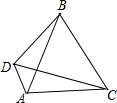 在△ABC中,BC=BA,D是△ABC外一点,且∠BCD=∠BAD=60°,求证:BC=CD+DA.
在△ABC中,BC=BA,D是△ABC外一点,且∠BCD=∠BAD=60°,求证:BC=CD+DA.