题目内容
13.在平面直角坐标系中,A(0,3),B(4,1),以AB为斜边作等腰Rt△ABC,求直角顶点C的坐标.分析 以AB为直径作⊙F,过圆心F作AB的垂直平分线,与⊙F的交点分别为C1,C2,利用利用勾股定理可知点C1符合题意,最后利用全等三角形可求出点C2的坐标.
解答 解:以AB为直径作⊙F交x轴与点C1和点D,过点F作FG⊥x轴于点G,
∵A(0,3),B(4,1),
∴利用中点公式可以求出F(2,2),
由勾股定理求出:AB=$2\sqrt{5}$,
∴FG=2,
∵C1F=$\frac{1}{2}$AB=$\sqrt{5}$,
∴由勾股定理可求出:C1G=1,
∴C1的坐标为(1,0),
∴由勾股定理可求得:C1B=$\sqrt{10}$,
∵C1B2=C1F2+BF2,
∴△C1FB是直角三角形,
∵C1F=BF,
∴∠C1BF=45°,
∴△AC1B是等腰直角三角形,
连接C1F,并延长交⊙F于点C2,连接C2D,
∴∠C1DC2=90°,
∴由中位线定理可知:C2D=2FG=4,
∴由勾股定理可知:C1D=2,
∴OD=3,
∴C2的坐标为(3,4),
综上所述,点C的坐标为(1,0)或(3,4).
点评 本题考查等腰三角形的性质,涉及圆周角定理,勾股定理及其逆定理等知识,综合程度较高.

练习册系列答案
相关题目
8.关于x的方程mx2+(m-1)x+m=0有实根,则实数m的取值范围是( )
| A. | {m|-1<m<$\frac{1}{3}$} | B. | {m|-1≤m≤$\frac{1}{3}$} | C. | {m|-1≤m≤$\frac{1}{3}$且m≠0} | D. | {m|m≤-1或m≥$\frac{1}{3}$} |
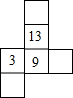 如图是一个立方体的平面展开图形,每个面上都有一个自然数,且相对的两个面上两数之和都相等,若13、9、3的对面的数分别是a、b、c,则a2+b2+c2-ab-ac-bc的值为76.
如图是一个立方体的平面展开图形,每个面上都有一个自然数,且相对的两个面上两数之和都相等,若13、9、3的对面的数分别是a、b、c,则a2+b2+c2-ab-ac-bc的值为76. 某中学八(1)班共50名同学开展了“我为灾区献爱心”捐款活动.小明将捐款情况进行了统计,并绘制成如图的条形统计图.
某中学八(1)班共50名同学开展了“我为灾区献爱心”捐款活动.小明将捐款情况进行了统计,并绘制成如图的条形统计图.