题目内容
12.解下列方程:(1)$\frac{2}{3}$+$\frac{x}{3x-1}$=$\frac{1}{9x-3}$
(2)$\frac{3}{x+1}$+$\frac{1}{x-1}$=$\frac{6}{{x}^{2}-1}$.
分析 两分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)去分母得:6x-2+3x=1,
解得:x=$\frac{1}{3}$,
经检验x=$\frac{1}{3}$是增根,分式方程无解;
(2)去分母得:3x-3+x+1=6,
解得:x=2,
经检验x=2是分式方程的解.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
相关题目
20.将(2-x)$\sqrt{\frac{1}{x-2}}$根号外的因式移到根号内,得( )
| A. | $\sqrt{x-2}$ | B. | $\sqrt{2-x}$ | C. | -2$\sqrt{2-x}$ | D. | -$\sqrt{x-2}$ |
7.镇江市教育局为帮助全市贫困师生举行“一日捐”活动,甲、乙两校教师各捐款60000元,已知“…”,设乙学校教师有x人,则可得方程$\frac{60000}{x}$-$\frac{60000}{(1+20%)x}$=20,根据此情景,题中用“…”表示的缺失的条件应补( )
| A. | 乙校教师比甲校教师人均多捐20元,且甲校教师的人数比乙校教师的人数多20% | |
| B. | 甲校教师比乙校教师人均多捐20元,且乙校教师的人数比甲校教师的人数多20% | |
| C. | 甲校教师比乙校教师人均多捐20元,且甲校教师的人数比乙校教师的人数多20% | |
| D. | 乙校教师比甲校教师人均多捐20元,且乙校教师的人数比甲校教师的人数多20% |

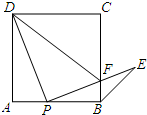 如图,点P是正方形ABCD边AB上一点(不与点A.B重合),连接PD并将线段PD绕点P顺时针方向旋转90°得到线段PE,PE交边BC于点F.连接BE、DF.
如图,点P是正方形ABCD边AB上一点(不与点A.B重合),连接PD并将线段PD绕点P顺时针方向旋转90°得到线段PE,PE交边BC于点F.连接BE、DF.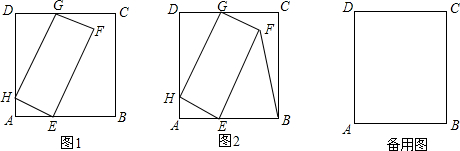
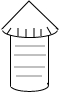 如图,粮仓的顶部是圆锥形状,这个圆锥底面圆的半径长为3m,母线长为6m,为防止雨水,需在粮仓顶部铺上油毡,如果油毡的市场价是每平方米10元钱,那么购买油毡所需要的费用是多少元(结果保留整数).
如图,粮仓的顶部是圆锥形状,这个圆锥底面圆的半径长为3m,母线长为6m,为防止雨水,需在粮仓顶部铺上油毡,如果油毡的市场价是每平方米10元钱,那么购买油毡所需要的费用是多少元(结果保留整数).