题目内容
4. 如图所示已知a,b,c在数轴上的位置如图所示:
如图所示已知a,b,c在数轴上的位置如图所示:(1)填空:a、b之间的距离为a-b;b、c之间的距离为b-c;a、c之间的距离为a-c;
(2)|a+b|-|c-b|+|b-a|;
(3)若c2=4,-b的倒数是它本身,a的绝对值的相反数是-2,求-a+2b-c-(a-4c-b)的值.
分析 利用数轴得出c<b<0<a,且|b|<|a|<|c|.
(1)利用数轴上的两点之间的距离求法:右边的点表示的数减去左边点表示的数即可;
(2)利用绝对值的意义化简合并即可;
(3)利用c2=4,-b的倒数是它本身,a的绝对值的相反数是-2,求得c=-2,b=-1,a=2,先化简再进一步代入求得答案即可.
解答 解:由数轴可知:c<b<0<a,且|b|<|a|<|c|.
(1)a、b之间的距离为a-b;b、c之间的距离为b-c;a、c之间的距离为a-c;
(2)|a+b|-|c-b|+|b-a|=a+b+c-b-b+a=2a-b+c;
(3)∵c2=4,-b的倒数是它本身,a的绝对值的相反数是-2,
∴c=-2,b=-1,a=2,
∴-a+2b-c-(a-4c-b)
=-a+2b-c-a+4c+b
=-2a+3b+3c
=-4-3-6
=-13.
点评 此题考查数轴,绝对值,相反数的意义,整式的加减,利用数轴得出a、b、c的数值的符号与大小是解决问题的关键.

练习册系列答案
相关题目
12.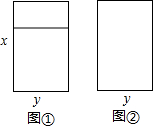 如图①,图②是宏达门窗厂制作的两种同大小的长方形铝合金窗框,已知窗框的长都是x米,窗框的宽都是y米.若王阿婆家装修需要图①窗框2个,图②窗框5个,则制作这些窗框需要铝合金多少米(接缝忽略不计)?
如图①,图②是宏达门窗厂制作的两种同大小的长方形铝合金窗框,已知窗框的长都是x米,窗框的宽都是y米.若王阿婆家装修需要图①窗框2个,图②窗框5个,则制作这些窗框需要铝合金多少米(接缝忽略不计)?
 如图①,图②是宏达门窗厂制作的两种同大小的长方形铝合金窗框,已知窗框的长都是x米,窗框的宽都是y米.若王阿婆家装修需要图①窗框2个,图②窗框5个,则制作这些窗框需要铝合金多少米(接缝忽略不计)?
如图①,图②是宏达门窗厂制作的两种同大小的长方形铝合金窗框,已知窗框的长都是x米,窗框的宽都是y米.若王阿婆家装修需要图①窗框2个,图②窗框5个,则制作这些窗框需要铝合金多少米(接缝忽略不计)?
9.已知两点A(-5,y1),B(3,y2)均在抛物线y=ax2+bx+c(a≠0)上,点C(x0,y0)是该抛物线的顶点.若y1<y2≤y0,则x0的取值范围是( )
| A. | x0>-1 | B. | x0<-1 | C. | -5<x0<-1 | D. | -1<x0<3 |
 已知有理数a、b、c在数轴上的位置如图所示,试化简|a|+|b|-|c|+|a-b|-|b+c|.
已知有理数a、b、c在数轴上的位置如图所示,试化简|a|+|b|-|c|+|a-b|-|b+c|. 如图,已知△ABC≌△FED,且BC=ED,那么AB与EF平行吗?为什么?
如图,已知△ABC≌△FED,且BC=ED,那么AB与EF平行吗?为什么? 已知如图:DE∥BC,并分别交AB、AC于点D、E.求证:△ADE∽△ABC.
已知如图:DE∥BC,并分别交AB、AC于点D、E.求证:△ADE∽△ABC.