题目内容
8．解不等式组$\left\{\begin{array}{l}{3x+1≤2（x+1）}\\{-x＜5x+12}\end{array}\right.$，并写出它的整数解．分析 分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集，最后求其整数解即可．
解答 解：解不等式3x+1≤2（x+1），得：x≤1，
解不等式-x＜5x+12，得：x＞-2，
则不等式组的解集为：-2＜x≤1，
则不等式组的整数解为-1、0、1．
点评 本题考查不等式组的解法及整数解的确定．求不等式组的解集，应遵循以下原则：同大取较大，同小取较小，小大大小中间找，大大小小解不了．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
如图，在△ABC中，AB=AC，点D在BC上，BD=DC，过点D作DE⊥AC，垂足为E，⊙O经过A，B，D三点．
13．
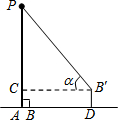小明利用测角仪和旗杆的拉绳测量学校旗杆的高度．如图，旗杆PA的高度与拉绳PB的长度相等．小明将PB拉到PB′的位置，测得∠PB′C=α（B′C为水平线），测角仪B′D的高度为1米，则旗杆PA的高度为（ ）
小明利用测角仪和旗杆的拉绳测量学校旗杆的高度．如图，旗杆PA的高度与拉绳PB的长度相等．小明将PB拉到PB′的位置，测得∠PB′C=α（B′C为水平线），测角仪B′D的高度为1米，则旗杆PA的高度为（ ）| A． | $\frac{1}{1-sinα}$ | B． | $\frac{1}{1+sinα}$ | C． | $\frac{1}{1-cosα}$ | D． | $\frac{1}{1+cosα}$ |
4．
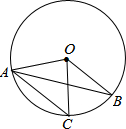如图，在⊙O中，弦AC与半径OB平行，若∠BOC=50°，则∠B的大小为（ ）
如图，在⊙O中，弦AC与半径OB平行，若∠BOC=50°，则∠B的大小为（ ）| A． | 25° | B． | 30° | C． | 50° | D． | 60° |
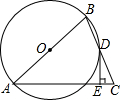
1．
如图，⊙O的圆心角∠BOC=112°，点D在弦BA的延长线上且AD=AC，则∠D的度数为（ ）
如图，⊙O的圆心角∠BOC=112°，点D在弦BA的延长线上且AD=AC，则∠D的度数为（ ）| A． | 28° | B． | 56° | C． | 30° | D． | 41° |