题目内容
8.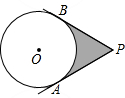 如图,P为⊙O外一点,PA,PB是⊙O的切线,A,B为切点,PA=$\sqrt{3}$,∠P=60°,则图中阴影部分的面积为$\sqrt{3}$-$\frac{1}{3}$π.
如图,P为⊙O外一点,PA,PB是⊙O的切线,A,B为切点,PA=$\sqrt{3}$,∠P=60°,则图中阴影部分的面积为$\sqrt{3}$-$\frac{1}{3}$π.
分析 连结PO交圆于C,根据切线的性质可得∠OAP=90°,根据含30°的直角三角形的性质可得OA=1,再求出△PAO与扇形AOC的面积,由S阴影=2×(S△PAO-S扇形AOC)则可求得结果.
解答  解:连结AO,连结PO交圆于C.
解:连结AO,连结PO交圆于C.
∵PA,PB是⊙O的切线,A,B为切点,PA=$\sqrt{3}$,∠P=60°,
∴∠OAP=90°,OA=1,
∴S阴影=2×(S△PAO-S扇形AOC)
=2×($\frac{1}{2}$×1×$\sqrt{3}$-$\frac{60×π×1}{360}$)
=$\sqrt{3}$-$\frac{1}{3}$π.
故答案为:$\sqrt{3}$-$\frac{1}{3}$π.
点评 此题考查了切线长定理,直角三角形的性质,扇形面积公式等知识.此题难度中等,注意数形结合思想的应用.

练习册系列答案
相关题目
3.在数轴上表示不等式2(1-x)<4的解集,正确的是( )
| A. |  | B. |  | C. |  | D. |  |
17. 如图所示的三视图所对应的几何体是( )
如图所示的三视图所对应的几何体是( )
 如图所示的三视图所对应的几何体是( )
如图所示的三视图所对应的几何体是( )| A. |  | B. |  | C. |  | D. |  |
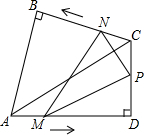 如图,在同一平面上,两块斜边相等的直角三角板Rt△ABC和Rt△ADC拼在一起,使斜边AC完全重合,且顶点B,D分别在AC的两旁,∠ABC=∠ADC=90°,∠CAD=30°,AB=BC=4cm
如图,在同一平面上,两块斜边相等的直角三角板Rt△ABC和Rt△ADC拼在一起,使斜边AC完全重合,且顶点B,D分别在AC的两旁,∠ABC=∠ADC=90°,∠CAD=30°,AB=BC=4cm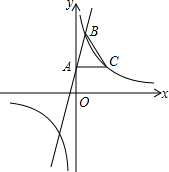 如图,在平面直角坐标系xOy中,一次函数y=3x+2的图象与y轴交于点A,与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象交于点B,且点B的横坐标为1.过点A作AC⊥y轴交反比例函数y=$\frac{k}{x}$(k≠0)的图象于点C,连接BC.
如图,在平面直角坐标系xOy中,一次函数y=3x+2的图象与y轴交于点A,与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象交于点B,且点B的横坐标为1.过点A作AC⊥y轴交反比例函数y=$\frac{k}{x}$(k≠0)的图象于点C,连接BC.