题目内容
18.太原市公共自行车的建设速度、单日租骑量等四项指标稳居全国首位.公共自行车车桩的截面示意图如图所示,AB⊥AD,AD⊥DC,点B,C在EF上,EF∥HG,EH⊥HG,AB=80cm,AD=24cm,BC=25cm,EH=4cm,则点A到地面的距离是$\frac{404}{5}$cm.
分析 分别过点A作AM⊥BF于点M,过点C作CN⊥AB于点N,利用勾股定理得出BN的长,再利用相似三角形的判定与性质得出即可.
解答 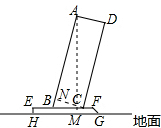 解:过点A作AM⊥BF于点M,过点C作CN⊥AB于点N,
解:过点A作AM⊥BF于点M,过点C作CN⊥AB于点N,
∵AD=24cm,则NC=24cm,
∴BN=$\sqrt{B{C}^{2}-N{C}^{2}}$=$\sqrt{2{5}^{2}-2{4}^{2}}$=7(cm),
∵∠AMB=∠CNB=90°,∠ABM=∠CBN,
∴△BNC∽△BMA,
∴$\frac{AB}{BC}$=$\frac{AM}{CN}$,
∴$\frac{80}{25}$=$\frac{AM}{24}$,
则:AM=$\frac{16×24}{5}$=$\frac{384}{5}$,
故点A到地面的距离是:$\frac{384}{5}$+4=$\frac{404}{5}$(m).
故答案为:$\frac{404}{5}$.
点评 此题主要考查了勾股定理的应用以及相似三角形的判定与性质,得出△BNC∽△BMA是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.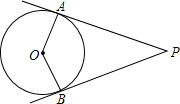 如图,点P在⊙O外,PA、PB分别与⊙O相切于A、B两点,∠P=50°,则∠AOB等于( )
如图,点P在⊙O外,PA、PB分别与⊙O相切于A、B两点,∠P=50°,则∠AOB等于( )
 如图,点P在⊙O外,PA、PB分别与⊙O相切于A、B两点,∠P=50°,则∠AOB等于( )
如图,点P在⊙O外,PA、PB分别与⊙O相切于A、B两点,∠P=50°,则∠AOB等于( )| A. | 150° | B. | 130° | C. | 155° | D. | 135° |
8.若代数式$\frac{1}{x-1}$+$\sqrt{x}$有意义,则实数x的取值范围是( )
| A. | x≠1 | B. | x≥0 | C. | x≠0 | D. | x≥0且x≠1 |
 由若干个相同的小正方体组合而成的一个几何体的三视图如图所示,则组成这个几何体的小正方体的个数是( )
由若干个相同的小正方体组合而成的一个几何体的三视图如图所示,则组成这个几何体的小正方体的个数是( ) 如图,在同一平面上,两块斜边相等的直角三角板Rt△ABC和Rt△ADC拼在一起,使斜边AC完全重合,且顶点B,D分别在AC的两旁,∠ABC=∠ADC=90°,∠CAD=30°,AB=BC=4cm
如图,在同一平面上,两块斜边相等的直角三角板Rt△ABC和Rt△ADC拼在一起,使斜边AC完全重合,且顶点B,D分别在AC的两旁,∠ABC=∠ADC=90°,∠CAD=30°,AB=BC=4cm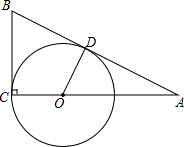 如图,在Rt△ACB中,∠ACB=90°,点O是AC边上的一点,以O为圆心,OC为半径的圆与AB相切于点D,连接OD.
如图,在Rt△ACB中,∠ACB=90°,点O是AC边上的一点,以O为圆心,OC为半径的圆与AB相切于点D,连接OD.