题目内容
2.下列命题是真命题的是( )| A. | 若分式$\frac{{x}^{2}-4}{2x-4}$的值为零,则x=±2 | |
| B. | 一组对边平行,一组邻角互补的四边形是平行四边形 | |
| C. | 顺次连接四边形四边中点所得到的四边形是平行四边形 | |
| D. | 三角形的三条角平分线相交于一点,并且这一点到三角形三个顶点的距离相等 |
分析 根据分式为0的条件、平行四边形的判定定理、三角形中位线定理、角平分线的性质定理判断即可.
解答 解:若分式$\frac{{x}^{2}-4}{2x-4}$的值为零,则x=-2,A是假命题;
一组对边平行,一组邻角互补的四边形不一定是平行四边形,如梯形,B是假命题;
顺次连接四边形四边中点所得到的四边形是平行四边形,C是真命题;
三角形的三条角平分线相交于一点,并且这一点到三角形三边的距离相等,D是假命题,
故选:C.
点评 本题考查的是命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠BEF,若∠1=50°,则∠2的度数为多少?
如图,已知AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠BEF,若∠1=50°,则∠2的度数为多少?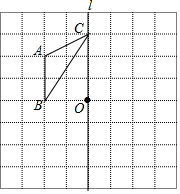 如图,在正方形网格中,点A、B、C、O都在格点上,直线l过点C、O两点.
如图,在正方形网格中,点A、B、C、O都在格点上,直线l过点C、O两点.
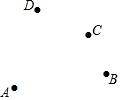 如图,平面上有A、B、C、D四个点,根据下列语句画图.
如图,平面上有A、B、C、D四个点,根据下列语句画图.