题目内容
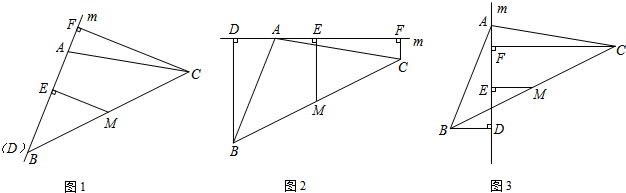
已知△ABC中,M为BC的中点,直线m绕点A旋转,过B、M、C分别作BD⊥m于D,ME⊥m于E,CF⊥m于F.
(1)当直线m经过B点时,如图1,易证EM=
CF.(不需证明)
(2)当直线m不经过B点,旋转到如图2、图3的位置时,线段BD、ME、CF之间有怎样的数量关系?请直接写出你的猜想,并选择一种情况加以证明.
(1)当直线m经过B点时,如图1,易证EM=
| 1 |
| 2 |
(2)当直线m不经过B点,旋转到如图2、图3的位置时,线段BD、ME、CF之间有怎样的数量关系?请直接写出你的猜想,并选择一种情况加以证明.

考点:旋转的性质,全等三角形的判定与性质,梯形中位线定理
专题:证明题
分析:(1)利用垂直于同一直线的两条直线平行得出ME∥CF,进而利用中位线的性质得出即可;
(2)根据题意得出图2的结论为:ME=
(BD+CF),图3的结论为:ME=
(CF-BD),进而利用△DBM≌△KCM(ASA),即可得出DB=CK,DM=MK即可得出答案.
(2)根据题意得出图2的结论为:ME=
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:(1)如图1,
解:(1)如图1,
∵ME⊥m于E,CF⊥m于F,
∴ME∥CF,
∵M为BC的中点,
∴E为BF中点,
∴ME是△BFC的中位线,
∴EM=
CF.
(2)图2的结论为:ME=
(BD+CF),
图3的结论为:ME=
(CF-BD).
图2的结论证明如下:连接DM并延长交FC的延长线于K
又∵BD⊥m,CF⊥m
∴BD∥CF
∴∠DBM=∠KCM
在△DBM和△KCM中
,
∴△DBM≌△KCM(ASA),
∴DB=CK,DM=MK
由题意知:EM=
FK,
∴ME=
(CF+CK)=
(CF+DB)
图3的结论证明如下:连接DM并延长交FC于K
又∵BD⊥m,CF⊥m
∴BD∥CF
∴∠MBD=∠KCM
在△DBM和△KCM中
,
∴△DBM≌△KCM(ASA)
∴DB=CK,DM=MK,
由题意知:EM=
FK,
∴ME=
(CF-CK)=
(CF-DB).
 解:(1)如图1,
解:(1)如图1,∵ME⊥m于E,CF⊥m于F,
∴ME∥CF,
∵M为BC的中点,
∴E为BF中点,
∴ME是△BFC的中位线,
∴EM=
| 1 |
| 2 |
(2)图2的结论为:ME=
| 1 |
| 2 |
图3的结论为:ME=
| 1 |
| 2 |
图2的结论证明如下:连接DM并延长交FC的延长线于K
又∵BD⊥m,CF⊥m
∴BD∥CF
∴∠DBM=∠KCM
在△DBM和△KCM中
|
∴△DBM≌△KCM(ASA),
∴DB=CK,DM=MK
由题意知:EM=
| 1 |
| 2 |
∴ME=
| 1 |
| 2 |
| 1 |
| 2 |
图3的结论证明如下:连接DM并延长交FC于K
又∵BD⊥m,CF⊥m
∴BD∥CF
∴∠MBD=∠KCM
在△DBM和△KCM中
|
∴△DBM≌△KCM(ASA)
∴DB=CK,DM=MK,
由题意知:EM=
| 1 |
| 2 |
∴ME=
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题主要考查了旋转的性质以及全等三角形的判定与性质等知识,得出△DBM≌△KCM(ASA)是解题关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
 已知二次函数y=a(x-1)2+c的图象如图,则一次函数y=ax+c的大致图象可能是( )
已知二次函数y=a(x-1)2+c的图象如图,则一次函数y=ax+c的大致图象可能是( )



 在平面直角坐标系中,已知点A(-3,1),B(-1,0),C(-2,-1),请在图中画出△ABC,并画出与△ABC关于y轴对称的图形.
在平面直角坐标系中,已知点A(-3,1),B(-1,0),C(-2,-1),请在图中画出△ABC,并画出与△ABC关于y轴对称的图形.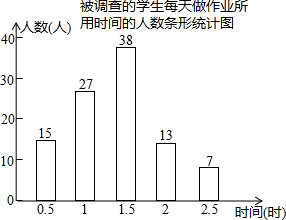 某校学生会为了解本校学生每天做作业所用时间情况,采用问卷的方式对一部分学生进行调查,在确定调查对象时,大家提出以下几种方案:
某校学生会为了解本校学生每天做作业所用时间情况,采用问卷的方式对一部分学生进行调查,在确定调查对象时,大家提出以下几种方案: 小强和小明去测量一座古塔的高度,他们在离古塔60米的A处,用测角仪器测得塔顶的仰角为30°,若测角仪器高AD=1.5米,则古塔BE的高为
小强和小明去测量一座古塔的高度,他们在离古塔60米的A处,用测角仪器测得塔顶的仰角为30°,若测角仪器高AD=1.5米,则古塔BE的高为